物質の熱的性質 1
ここまで,熱力学の基礎理論を学んできました。ここからは実際の物質や化学反応に熱力学を適用してみましょう。
標準状態
はじめに標準状態(standard state)を定義します(速習編 > 標準状態も併せて参照のこと)。
温度 $T$ における物質の標準状態とは,温度 $T$,標準状態圧力 $p^\circ$ における,その物質の純粋な状態または仮想的な状態である。
上付きの $\circ$ は標準状態を表す記号です。標準状態には温度は定められておらず,都度指定する必要がありますが,習慣により温度の指定が省略してあるときは $T=298.15\unit{K}$ です。物質の標準状態を規定する際の標準圧力である標準状態圧力(standard state pressure)SSP は,現在では $10^5\unit{Pa}=1\unit{bar}$ と決められています(1982 年以前は $101.325\unit{kPa}$ を SSP としていました)。ただし,用途によって他の圧力を用いた方が都合がよい場合もあります。例えば,物質の沸点は $1\unit{bar}=0.987\unit{atm}$ を基準とした標準沸点(standard boiling point)よりも,標準大気圧($101.325\unit{kPa} = 1\unit{atm}$)を圧力の基準とした通常沸点(normal boiling point)を用いることが一般的です。「仮想的な状態」というのは,例えば SSP($1\unit{bar}$)で $400\unit{K}$ の条件では,水は(熱平衡状態で)液体としては存在できませんが,液体であると仮定した場合の熱力学諸量(定圧熱容量や,標準エントロピーなど)を理論的に求めることはできます。したがってこの場合の水(液体)は $400\unit{K}$ における水の「仮想的な状態」です。
基準状態
SSP($1\unit{bar}$),指定温度で最も安定な状態にある元素の単体を,その元素の基準状態(reference state)といいます。
例えば $298.15\unit{K}$ において,(元素としての)窒素は,気体の窒素分子($\ce{N2}$)として存在するのが最も安定ですので,窒素の基準状態は気体の $\ce{N2}$ です。炭素の単体には黒鉛(graphite),ダイヤモンドの他,フラーレン($\ce{C60}$)やカーボンナノチューブなどいくつかの同素体がありますが,炭素の基準状態は黒鉛です。
例外がひとつあり,リン(phosphorus,$\ce{P}$)は $298.15\unit{K}$ で黒リンが最も安定な状態ですが,黒リンは結晶多形であるため,熱力学データの再現性確保が難しい一方で,白リンは分子性の $\ce{P4}$ の構造をもち,準安定であるものの,実験の再現性が良好であることから,白リンが基準状態として採用されています。
物理変化に伴うエンタルピー変化
標準状態において,物質が液体から気体に状態変化する際に必要な熱量をその物質の蒸発熱または気化熱といいます。通常,液体を気体に変えるには外界から熱を与える必要があり,この熱量が蒸発熱です。同じことをエンタルピー変化で表す場合は標準蒸発エンタルピー(standard vaporization enthalpy)$\DHo{vap}$ といいます。両者の概念は完全には同じではありませんが,数値としては蒸発熱と蒸発エンタルピーは等しくなります。例えば,水の通常沸点($373.15\unit{K}$)における標準蒸発エンタルピーは,$\DHo{vap}(373.15\unit{K})=+40.656\kJmol$ です。
同様に,標準状態において固体から液体への状態変化に伴うエンタルピー変化は標準融解エンタルピー(standard fusion enthalpy)$\DHo{fus}$ といい,水の通常融点における標準融解エンタルピーは,$\DHo{fus}(273.15\unit{K})=+6.01\kJmol$ です。
他にも,昇華(sublimation)であれば,標準昇華エンタルピー $\DHo{sub}$ や,斜方硫黄から単斜硫黄への変化のような,結晶構造の変化に伴うエンタルピー変化である 標準転移エンタルピー $\DHo{tr}$ などもあります。それぞれに対して,融解熱,昇華熱,転移熱などが対応します。
標準状態において,イオン結晶の静電的な引力を断ち切って,イオンをバラバラの気体状態にするときのエンタルピー変化を標準格子エンタルピー(standard lattice enthalpy)$\DHo{latt}$ といいます。例えば塩化ナトリウムであれば,$\ce{NaCl(s)}$ を $\ce{Na+(g) + Cl-(g)}$ にするのに必要な熱量です。塩化ナトリウムを例に各種エンタルピーの関係をボルン・ハーバーサイクル(Born-Haber cycle)で以下に示します。
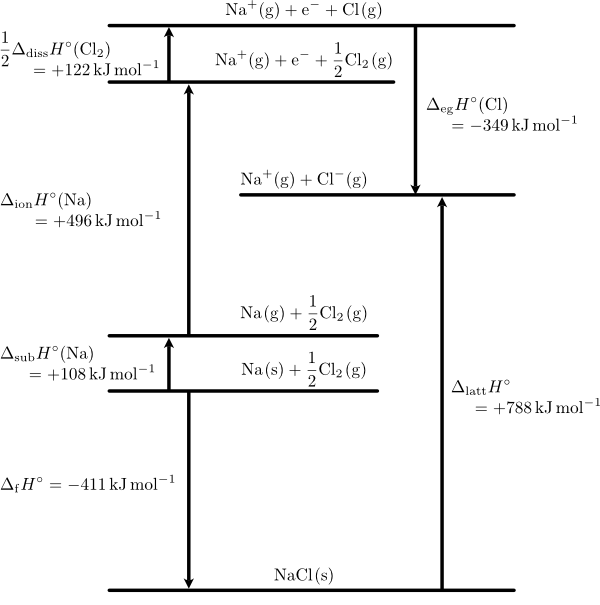
塩化ナトリウムのボルン・ハーバーサイクル
図中の $\DHo{eg}(\ce{Cl})$ は塩素原子の標準電子獲得エンタルピー(standard electron gain enthalpy)で,電子親和力(electron affinity)$\Ae$(または $E_\mathrm{a}$)とは符号が反転します。気体の塩素分子を塩素原子に解離するのに必要なエンタルピーは標準結合解離エンタルピー(standard bond dissociation enthalpy)$\DHo{diss}$ で,$\DHo{diss}(\ce{Cl2})=242.851\pm 0.096\kJmol$ と報告されていますが,ここではその半量が関わりますので $+122\kJmol$ となっています。
分子性結晶の場合は,分子の状態でバラバラにするのであれば,既に述べた昇華エンタルピーがこれに相当しますが,さらに原子にまでバラバラにするのであれば,標準原子化エンタルピー $\DHo{at}$ が使われます。昇華エンタルピーが分子間力を反映するのに対して,原子化エンタルピーは原子間の結合エネルギーの情報を含みます。金属の固体を気体の原子状にする場合のエンタルピー変化も原子化エンタルピーで,この場合は金属結合エネルギーが反映されます。
燃焼エンタルピー
一般に可燃物質と酸素との反応でおこる,光と熱の発生を伴う化学反応を燃焼(combustion)といい,燃焼に伴い発生した熱量を燃焼熱と言います。プロパン $\ce{C3H8}$ を完全燃焼して二酸化炭素と水が生じるとき,$1\unit{mol}$ のプロパンの完全燃焼によって,$+2220\unit{kJ}$ の熱量が外界に放出されます(速習編 > プロパンの燃焼)。
この化学式では,燃焼で生じた右辺の水は $\ce{H2O(l)}$ と書いて,液体であることを示しています。プロパンを燃焼して生じるのは水蒸気ですが,反応後に指定した温度(通常は $298.15\unit{K}$)に戻した状態での熱量の収支を考えることになっており,この場合は水蒸気が凝縮して液体の水になる分の熱量の移動(この場合は発熱)も燃焼熱 $+2220\unit{kJ\,mol^{-1}}$ の中に含まれています。
燃焼熱は外界視点での熱の移動(発熱で正値)ですが,熱力学では系を中心に議論することになりますので,定圧条件での系の熱量の出入りであるエンタルピー $H$ で表す場合には符号が逆転して,プロパンの標準燃焼エンタルピー $\DHo{c}$ は $-2220\unit{kJ\,mol^{-1}}$ ということになります。蒸発熱などの場合は,エンタルピーと符号を含め同じ数値になりましたが,燃焼熱の場合は符号が反転する点に注意が必要です。エンタルピーは常に系の視点での変化,〇〇熱の場合は系視点の場合もあれば,外界視点の場合もあります。以下に例としていくつかの物質の標準燃焼エンタルピーをまとめます。
| $\DHo{c}\,/\unit{kJ\,mol^{-1}}$ | |||
|---|---|---|---|
| carbon (graphite) | 炭素(黒鉛) | $\ce{C(graphite)}$ | $-393.5$ |
| hydrogen | 水素 | $\ce{H2}$ | $-285.8$ |
| methanol | メタノール | $\ce{CH3OH}$ | $-725.9$ |
| methane | メタン | $\ce{CH4}$ | $-890.5$ |
| propane | プロパン | $\ce{C3H8}$ | $-2219.9$ |
生成エンタルピー
構成元素の基準状態から,物質が生成するときのエンタルピー変化を標準生成エンタルピー(standard formation enthalpy)$\DHo{f}$ と言います。生成熱の場合は符号が反転するのは燃焼熱と同じです。この際,基準状態にある元素単体の標準生成エンタルピーは常にゼロであると定義します。これは,単体から単体を生成する(何もしない)ときのエンタルピー変化はゼロと言っているだけですので,複雑な話ではありません。
例えば,気体の二酸化炭素 $\ce{CO2(g)}$ の標準生成エンタルピーは,炭素と酸素の基準状態である黒鉛 $\ce{C(graphite)}$ と酸素分子 $\ce{O2(g)}$ から $\ce{CO2(g)}$ が生成する際のエンタルピー変化に相当し,これはすなわち黒鉛の標準燃焼エンタルピー $\DHo{c}$ ですので,上の表から $\DHo{f}(\ce{CO2}) = -393.5\kJmol$ となります。
同様に液体の水 $\ce{H2O(l)}$ の標準生成エンタルピーは,水素 $\ce{H2(g)}$ の標準燃焼エンタルピーから求まり,$\DHo{f}(\ce{H2O}) = -285.8\kJmol$ となります。
このように,単体酸化物の標準生成エンタルピーは,元となる単体の標準燃焼エンタルピーとイコールですので,実験により直接求めることができます。一方で,単体酸化物ではない物質の標準生成エンタルピーを求めるのは簡単ではありません。例えば,メタノール $\ce{CH3OH}$ の生成エンタルピーは,定義に従えば単体の黒鉛,水素,酸素からメタノールを生成するときのエンタルピー変化ということになりますが,次式で示すような黒鉛,水素,酸素を混ぜてメタノールを合成する実験というのは容易ではありません(これらを混ぜて加熱したところでメタノールは生成しません)。
しかし,このような場合でも,メタノールの標準燃焼エンタルピーであれば実験により求めることが可能で,上の表から $\DHo{c}(\ce{CH3OH}) = -725.9\kJmol$ と分かっています。
すると,メタノールの標準生成エンタルピーは,メタノール,黒鉛,水素の標準燃焼エンタルピーを使って,間接的に求めることができます。
これが成立するのは,上の化学式で $\eqref{fch3oh} = \eqref{fco2} + 2\times\eqref{fh2o} - \eqref{cch3oh}$ であり,また,単体である $\ce{C(graphite)}$ と $\ce{O2(g)}$ の標準生成エンタルピーをゼロとしているから,そして,化学反応における反応熱の総和は,反応の始状態と終状態だけで決まり,途中の経路に依らない(どのように迂回してもゴールが同じであれば同じ結果になる)ということを定めたヘスの法則(Hess' law)が成立しているからです。

メタノールの標準生成エンタルピー
このように,実験で求めた標準燃焼エンタルピーを使って標準生成エンタルピーが求まります。ただし,一般にデータベースなどでは,燃焼エンタルピーよりは,こうして求めた標準生成エンタルピーの方が掲載されていることが多いです。上では(話の流れ上)燃焼エンタルピーから生成エンタルピーを求めたという形で書きましたが,実際のところはデータベースでメタノール,$\ce{CO2(g)}$,$\ce{H2O(l)}$ の $\DHo{f}$ を確認し,それを使って $\DHo{c}$ を計算しています。
反応エンタルピー
化学反応に関わる物質の生成エンタルピーが分かっていれば,その化学反応によるエンタルピー変化である標準反応エンタルピー(standard reaction enthalpy)$\DHo{r}$ を求めることができます。例としてベンゼン $\ce{C6H6(l)}$ に水素を付加してシクロヘキサン $\ce{C6H12(l)}$ を得る反応を考えます。
液体のベンゼンとシクロヘキサンの標準生成エンタルピーはそれぞれ $49.1\kJmol$,$-156.4\kJmol$ であるとデーターベースに記載されています。よってこの反応の標準反応エンタルピーはシクロヘキサン(液体)の生成エンタルピーから,ベンゼン(液体)生成エンタルピーを引いた値になります(水素の生成エンタルピーはゼロです)。
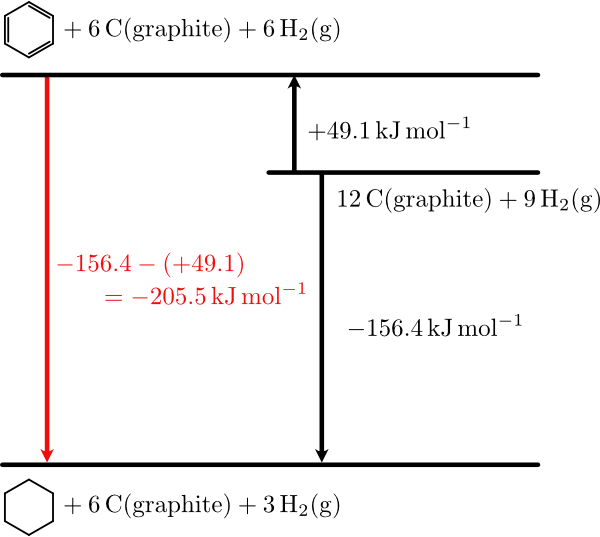
ベンゼンの水素化によるシクロヘキサンの生成反応
イオンの生成エンタルピー
イオンが生成する際の生成エンタルピーも定義することができます。ただし,純粋なイオンは取り出せませんので,基準を一つ定めて,基準からのエンタルピー差をとる必要があります。
イオンの標準生成エンタルピー $\DHo{f}$ は,水和したプロトンの標準生成エンタルピーを温度にかかわらずゼロと定義し,これを基準とした相対値を用いる。
例えば,$\ce{HBr(aq)}$ の標準生成エンタルピーは $-121.6\kJmol$ と報告されています。
$\ce{HBr}$ は強酸で水中で完全電離しますので,$\ce{HBr(aq)}$ の生成エンタルピーはすなわち $\DHo{f}(\ce{H+,aq})$ と $\DHo{f}(\ce{Br-,aq})$ の和となります。前者はゼロと定義されているので,臭化物イオンの標準生成エンタルピーは $\DHo{f}(\ce{Br-,aq}) = -121.6\kJmol$ と求まります。

