物質の熱的性質 2
熱力学データの温度依存性
標準状態には温度の指定はありませんので,ある物理量の標準状態での値は温度ごとに異なる値となります。表記を省略すれば慣例により $298.15\unit{K}$ とみなされますが,指定するのであれば $\DHo{}_{373.15}$,$\So_{500}$ のように表記します。
データベースには様々な物質の標準状態における熱力学データが記載されていますが,実験値としての温度依存性が記載されている物質は限られており,しかもいくつかの代表的な温度についての記載しかありません。NIST(National Institute of Standards and Technology)では色々な物質の熱力学データを NIST Chemistry WebBook として公開しており,その中に温度依存性を求めるための近似式が記載されています。
以下は NIST のサイトで液体の水の熱力学データを参照した結果の引用です。
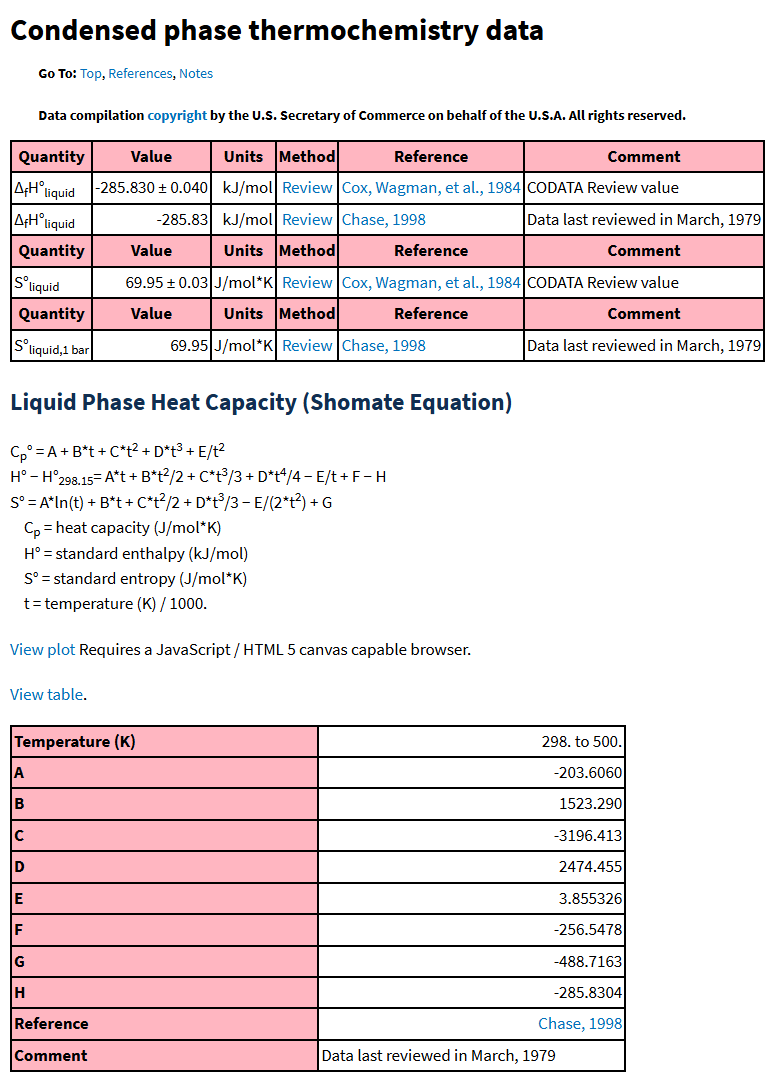
水(液体)の熱力学データ(NIST Chemistry WebBook より引用)
このページの上部には $298.15\unit{K}$ における液体の水の標準生成エンタルピーや標準エンタルピーが掲載されています(値はリファレンスにより少しずつ異なる)。その下に定圧熱容量,エンタルピー,エントロピーの温度依存性を求めるための近似式が与えられています。近似式中の A ~ H のパラメータはその下の表にあります。この近似式を使って熱力学データの温度依存性をプロットしたのが以下のグラフです。このように,温度依存性を近似式で関数化することで,積分計算も容易に行うことができるようになります。
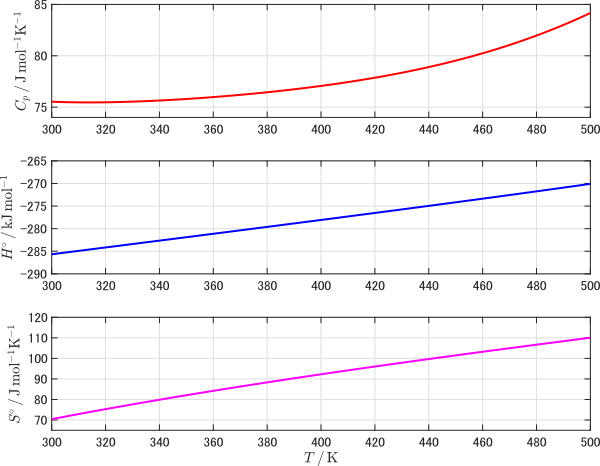
水(液体)の熱力学データの温度依存性
生成ギブズエネルギー
エンタルピー同様に標準生成ギブズエネルギー(standard Gibbs free energy of formation)も定義することができます。具体例を示した方が分かりやすいと思いますので,いくつかの気体分子の熱力学データをデータベースより以下に引用します。
| $\DHo{f}(\mathrm{g})\,/\kJmol$ | $\DGo{f}(\mathrm{g})\,/\kJmol$ | $\So(\mathrm{g})\,/\mathrm{J\,mol^{-1}K^{-1}}$ | $C_p(\mathrm{g})\,/\mathrm{J\,mol^{-1}K^{-1}}$ | ||
|---|---|---|---|---|---|
| ammonia | $\ce{NH3}$ | $-45.9$ | $-16.4$ | $192.8$ | $35.1$ |
| carbon dioxide | $\ce{CO2}$ | $-393.5$ | $-394.4$ | $213.8$ | $37.1$ |
| carbon monoxide | $\ce{CO}$ | $-110.5$ | $-137.2$ | $197.7$ | $29.1$ |
| hydrogen | $\ce{H2}$ | $0.0$ | $130.7$ | $28.8$ | |
| nitrogen | $\ce{N2}$ | $0.0$ | $191.6$ | $29.1$ | |
| nitrogen dioxide | $\ce{NO2}$ | $33.2$ | $51.3$ | $240.1$ | $37.2$ |
| nitric oxide | $\ce{NO}$ | $91.3$ | $87.6$ | $210.8$ | $29.9$ |
| oxygen | $\ce{O2}$ | $0.0$ | $205.2$ | $29.4$ |
この表中で標準生成エンタルピーが $0.0$ と記載されている単体は,この状態が基準状態であることを示しています。この場合は気体状態 $(\mathrm{g})$ が基準状態ということです。ここでは省略しましたが,データベースには固体や液体の生成エンタルピーの欄もあるのですが,そちらには(基準状態ではないので)$0.0$ の記載はありません。また例えば,水銀 $\ce{Hg}$ の基準状態は $298.15\unit{K}$ で液体ですので,$\DHo{f}(\mathrm{l})$ の欄に $0.0$ と記載されており,一方で $\DHo{f}(\mathrm{g})$ の欄には $61.4$ の数字が書かれています。
窒素と水素からアンモニアが生成する反応を考えます。
この生成反応の標準エントロピー変化は,アンモニア,窒素,水素のそれぞれの標準エントロピーを(係数倍して)差し引きすると得られます。その結果をギブズエネルギーの定義である $G = H -TS$($\Delta G = \Delta H - T\Delta S$)に代入すると,$-16.37\kJmol$ となり,これが上の表の $\DGo{f}(\mathrm{g}) = -16.4\kJmol$ に対応しています。
アンモニアの生成反応は単体どうしの反応でしたが,反応に関わる物質の標準生成ギブズエネルギーが分かっていれば,化合物が反応する場合でも反応ギブズエネルギーを求めることができます。以下は一酸化窒素と酸素から二酸化窒素が生成する反応とそのギブズエネルギー変化です。
化学反応におけるギブズエネルギー変化
ギブズエネルギーとは定圧条件で取り出すことができる(系の体積変化以外の)仕事の最大値でしたが,化学反応におけるギブズエネルギー変化とは何を意味するのでしょうか。これは,化学反応に関わる各物質が潜在的に持っている定圧条件での化学反応の進行に伴って取り出せる仕事の最大値です。すなわち上式に従ってアンモニアが $1\unit{mol}$ 生成すると,系が持っていた「仕事の潜在能力」が $16.37\unit{kJ}$ だけ減るということになります。反応は,与えられた条件で,これ以上ギブズエネルギーを減らすことができなくなるまで進みます。すなわち,化学反応は $G$ が減る方向($\Delta G < 0$)に進み,(閉じた系全体の)$G$ が極小値に達する($\Delta G$ がゼロとなるような条件に達する)と,それ以上は反応がどちらに進んでも $G$ が増加することから,化学反応により仕事を取り出すことができなくなり,反応は見かけ上進行しなくなります。これが化学平衡に達した状態です。化学反応の方向性と化学平衡を決めているのは(エンタルピーではなく)ギブズエネルギーである点が重要です。
アンモニアの生成反応は閉じた系で起こりますが,見方を変えると,窒素や水素が系の外に出て行き,アンモニアが系の外から入ってきたと考えることもできます。よって,化学反応を考える際は開いた系を想定し,反応に関わる物質が系を出入りするときのギブズエネルギー変化を考えるのが便利です。イメージとしては物質を系から追い出す仕事,物質を系に取り入れる仕事の差し引きが反応ギブズエネルギー変化に相当するものです。
このような物質の出入りによるギブズエネルギー変化は開いた系の取り扱いになり,開いた系については概論編での学習を予定しています。

