酸化還元反応の方向
酸化還元反応は電子を受け取る反応と電子を渡す反応がセットで起こると説明しました。では二つの物質があり,それらが酸化還元反応を起こすとすると,どちらが酸化剤となって相手から電子を奪うのでしょうか。硫酸銅(II)水溶液に亜鉛片を入れたときの反応を考えてみましょう。銅(II)イオンは還元されて単体の銅が析出し,亜鉛は酸化されて亜鉛イオンとなって溶液中に溶け出します。金属樹の例として習った方も多いと思います。この反応は以下の二つの半反応式にわけて考えることができます。
ただし,半反応式は還元反応で記述するのが一般的ですので,その習慣に従って反応式\eqref{Znox}を書き直します。
反応式\eqref{Cured}と\eqref{Znred}の差 $\eqref{Cured}-\eqref{Znred}$ をとると全反応式が得られます。
ここで硫酸亜鉛(II)水溶液と銅片を用いて $\eqref{Znred}-\eqref{Cured}$ の反応式をつくるのではなくて反応式\eqref{ZnCudis}を求めたのは,私たちが $\ce{Zn}$ は $\ce{Cu}$ よりもイオンになりやすい(イオン化傾向が大きい)という知識を持っているからです。しかし,もしこの知識がなかったとしたら反応はどちらに進むか予測することはできるでしょうか。例えば $\ce{Zn}$ の代わりにカドミウム $\ce{Cd}$ だったら反応はどちらに進むかわかりますか?インジウム $\ce{In}$ とスカンジウム $\ce{Sc}$ の組み合わせではどうなりますか?毎回実験で確かめるというのも一つの手ではありますが,膨大な組み合わせに対して酸化還元反応が進行する向きが決まる原理を考える必要がありそうです。
電極電位
酸化還元反応がどちら向きに進行するのか,その基礎となる原理は講義 > 化学熱力学で学ぶように熱力学で取り扱います。ある(標準状態での)可逆反応を考えるとき,この反応は反応前後のギブズエネルギー変化 $\DGo{r}$ が負になる方向に進行します。なお物質の標準状態の条件は $10^5\unit{Pa} = 1\unit{bar}$ であると化学熱力学 > 標準状態で学びましたが,溶液の場合はこれに加え,溶液の構成成分の活量 $a$ が $1$ であるという条件が加わります。酸性溶液であればプロトンの活量も $1=10^0$ ですので $\pH\ 0$ が条件となります。温度は別途指定する必要がありますが,慣例により明記していない場合は $25\oC$($298.15\unit{K}$)です。
上の例であれば,反応式\eqref{ZnCudis}とその逆反応のどちらが $\DGo{r} < 0$ になるかを考えればよいわけです。となると $\DGo{r}$ の求め方が重要になってきますが,実はこの話は化学熱力学 > 酸化還元で既に取り扱った内容ですのでここでは結果だけを振り返ると,酸化還元反応では酸化還元反応に基づく二つの電極を用いて電池を組み立て,電極間に生じた電位差を測定することで次式の関係からギブズエネルギー変化を知ることができます。
$\nue$ はその酸化還元反応に関わる電子数,$F$ はファラデー定数,$\Eocell$ は標準電池電位でした。ただし,すべての組み合わせについて電池電位を求めるのは得策ではなく,各半反応に対して標準電極電位(standard electrode potential)を求めておいて,そこから必要に応じて組み合わせをつくるのでした。標準電極電位は標準還元電位(standard reduction potential)とも呼ばれます。そして半反応の標準電極電位を求めるのに必要な相手方の電極として標準水素電極(standard hydrogen electrode, SHE)が使われるのでした。
標準水素電極を用いて銅 $\ce{Cu}$ の標準電極電位を求める模式図を下に示します。この図で標準水素電極は左側の部分で,水素 $\ce{H2}$ が白金触媒上で酸化(銅の場合。相手によっては $\ce{H+}$ が還元)されますが,その電位を基準(ゼロ)として,右側に設置した電極の電極電位 $E$ を求めます。正確には $\pH\ 0$,$1\unit{bar}$ 水素ガスという条件での水素イオンの還元に対する $\DGo{r}$ を温度に関わらずゼロと定義し,そのときの電池電位を(右側の電極の)標準電極電位 $\Eo$ とします。また SHE 側で起こる反応が実際は還元であったとしても,常に SHE が負極(酸化が起こっている)とみなして,その違いは $\Eo$ の符号で表す約束になっていて,プロトンよりも還元されやすい化学種の $\Eo$ は正値,還元されにくい化学種の $\Eo$ は負値で表されます。$\ce{Cu}$ はプロトンを還元することができませんので $\ce{Cu}$ の $\Eo$ は正値,$\ce{Zn}$ はプロトンを還元して水素ガスが発生しますので $\Eo$ は負値という具合になります。
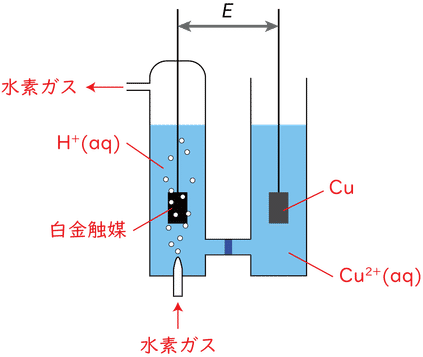
標準水素電極
このように標準水素電極に対する電極電位(還元電位)を色々な半反応に対して求めておけば,あとは必要な組み合わせの半反応を選んでそれぞれの電極電位を引き算して $\Eocell$ を求めれば,式\eqref{DGoEcell}に従って全反応のギブズエネルギー変化が求まります。右辺にマイナスがついていますので $\Eocell$ が正になる方向に反応が進行することに注意してください。代表的な還元反応について標準電極電位を以下に示します。より詳しくは資料 > 標準電極電位にまとめました。プロトンの電極電位は定義値です。
| Reaction | $\Eo /\unit{V}$ |
|---|---|
| $\ce{F2 + 2e- <=> 2F-}$ | $2.866$ |
| $\ce{Au^{3+} + 3e- <=> Au}$ | $1.498$ |
| $\ce{Pd^{2+} + 2e- <=> Pd}$ | $0.951$ |
| $\ce{Ag+ + e- <=> Ag}$ | $0.7996$ |
| $\ce{Cu^{2+} + 2e- <=> Cu}$ | $0.3419$ |
| $\ce{2H+ + 2e- <=> H2}$ | $0.0000$ |
| $\ce{Ni^{2+} + 2e- <=> Ni}$ | $-0.257$ |
| $\ce{Cd^{2+} + 2e- <=> Cd}$ | $-0.4030$ |
| $\ce{Zn^{2+} + 2e- <=> Zn}$ | $-0.7618$ |
| $\ce{Al^{3+} + 3e- <=> Al}$ | $-1.676$ |
| $\ce{Mg^{2+} + 2e- <=> Mg}$ | $-2.372$ |
| $\ce{Na+ + e- <=> Na}$ | $-2.71$ |
| $\ce{Ca^{2+} + 2e- <=> Ca}$ | $-2.868$ |
| $\ce{K+ + e- <=> K}$ | $-2.931$ |
| $\ce{Rb+ + e- <=> Rb}$ | $-2.98$ |
| $\ce{Cs+ + e- <=> Cs}$ | $-3.026$ |
| $\ce{Li+ + e- <=> Li}$ | $-3.0401$ |
この表の上にある還元反応ほど $\DGo{}$ が負に大きいので進みやすく,下にあるものほど進みにくいということになります。この表の中の組み合わせで電池を作ったとすると,表の上にあるのが正極となり,上の $\Eo$ から下の $\Eo$ を引くことで電池の起電力が求まります。ダニエル電池であれば銅板が正極で,起電力は $0.3419 - (-0.7618) = +1.1037\unit{V}$ となります。電池の起電力と電池電位の関係などについては次節以降で詳しく扱います。

