カルノーサイクル

ピストン付き密閉容器に気体を入れ，等温（熱の出入りがある）または断熱（熱の出入りがないので温度が変化する）の条件で気体を膨張または圧縮させる，以下のような一連の操作を考えます。ここでの気体は理想気体である必要はなく，作業物質（working substance）と呼ばれます。

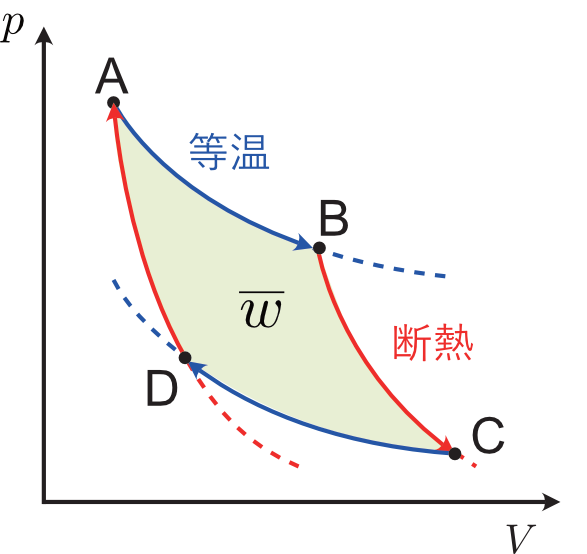
具体的な挙動は作業物質の種類によって変わりますが，原理的にはこの一連の操作で系は状態 A からぐるっと一周して，元の状態 A に戻ります。これは本編 > 理想気体の断熱変化で最後に紹介した $p\,\text{-}V$ 図から青線と赤線で囲まれた領域をどれでもよいので一つ選んだことに相当します。しかもすべての操作が準静的なので，各操作はすべて可逆で，このサイクルは ADCBA のように同じ道筋を通って逆に回すこともできます。このような準静的な熱機関をカルノーサイクル（Carnot cycle）と言います。

高温熱源と低温熱源を用意します（具体的な温度は定めませんが，これらは以降ずっと共通で用います）。上記のカルノーサイクルの例で言えば，高温熱源の温度が $T_\mathsf{A}\,(\,=T_\mathsf{B})$，低温熱源の温度が $T_\mathsf{C}\,(\,=T_\mathsf{D})$ であるという設定です。

作業物質が異なる二つのカルノーサイクルを考え，それぞれ $\mathsf{C}$，$\mathsf{C'}$ としましょう。$\mathsf{C}$ は高温熱源から熱量 $\color{red}{q_1}$ を受け取り，外界に仕事 $\overline{w}$ をして，低温熱源に熱量 $\color{blue}{q_2}$ を捨てます。第一法則により $\overline{w} = \color{red}{q_1}\ \color{black}{-}\ \color{blue}{q_2}$ です。一方，$\mathsf{C'}$ は高温熱源から熱量 $\color{red}{q_1'}$ を受け取り，外界に仕事 $\overline{w'}$ をして，低温熱源に熱量 $\color{blue}{q_2'}$ を捨てるとしましょう。$\overline{w'} = \color{red}{q_1'}\ \color{black}{-}\ \color{blue}{q_2'}$ です。赤色の $\color{red}{q}$ は系が受け取る熱量，青色の $\color{blue}{q}$ は系が捨てる熱量（どちらも正の値）と前節で約束したことを思い出しましょう。

高校理科編 > 熱力学第二法則で見たように，カルノーサイクルを 1 サイクル動かして得られる仕事は $p\,\text{-}V$ 平面でサイクルに囲まれた部分の面積に等しくなります。そこで $\mathsf{C'}$ については上手く調節して $\mathsf{C}$ と（形は違ってもよいので）面積が等しくなるようにしておきます。これで $\overline{w}=\overline{w'}$ となります。

カルノーサイクルは逆回転できますので，$\mathsf{C'}$ を逆回転させたサイクル $\mathsf{C'_{rev}}$ を考えてみましょう。これは外界からカルノーサイクル（の装置）に仕事 $w' = \overline{w'}$ を与えることで，低温熱源から熱量 $\color{red}{q_2'}$ を受け取り，高温熱源に熱量 $\color{blue}{q_1'}$ を渡すことに相当します。そこで，$\mathsf{C}$ と $\mathsf{C'_{rev}}$ を連結して，$\mathsf{C}$ で取り出した仕事 $\overline{w}$ を $\mathsf{C'_{rev}}$ に投入してみましょう。$\mathsf{C'}$ は $\overline{w}=\overline{w'}$ となるように調整してあるので，この連結カルノーサイクル全体の正味の仕事はゼロです。そしてサイクルを 1 周すると，低温熱源からトータルで $\color{red}{q_2'}\ \color{black}{-}\ \color{blue}{q_2}$ の熱量を受け取り，高温熱源にトータルで $\color{blue}{q_1'}\ \color{black}{-}\ \color{red}{q_1}$ の熱量を渡したことになります。下図の左の状況です。

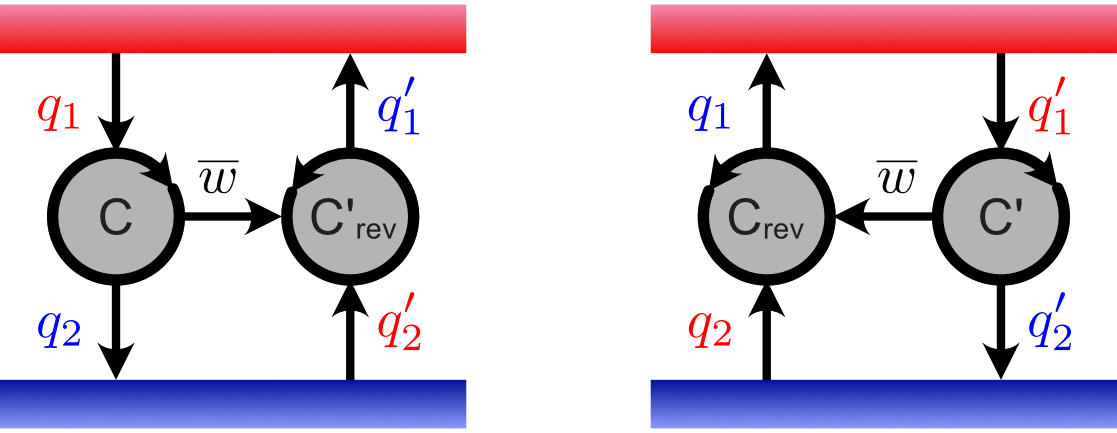
連結した二つのカルノーサイクル。右図は左図の各サイクルを逆回転させたもの。

第一法則より（仕事分は正味ゼロなので） $\color{blue}{q_1'}\ \color{black}{-}\ \color{red}{q_1}\ \color{black}{=}\ \color{red}{q_2'}\ \color{black}{-}\ \color{blue}{q_2}$ ですが，このとき $\color{blue}{q_1'}\ \color{black}{-}\ \color{red}{q_1}\ \color{black}{=}\ \color{red}{q_2'}\ \color{black}{-}\ \color{blue}{q_2}\ \color{black}{>}\ 0$ だったとすると，正味の仕事なしに低温熱源から高温熱源に熱を移したことになり，これはクラウジウスの原理（すなわち第二法則）に反します。私たちは第二法則を受け入れる立場ですから，これより次式を満たす要請が生じます。

一方，この連結カルノーサイクル全体を逆回転させるとどうなるでしょうか。上図の右の状況です。低温熱源からトータルで $\color{red}{q_2}\ \color{black}{-}\ \color{blue}{q_2'}$ の熱量を受け取り，高温熱源にトータルで $\color{blue}{q_1}\ \color{black}{-}\ \color{red}{q_1'}$ の熱量を渡したことになります。よって同様の議論から次式を満たす要請が生じます。

式\eqref{eq01}と式\eqref{eq02}を同時に満たす必要がありますので，結局 $q_1=q_1'$，$q_2=q_2'$ でなくてはなりません（熱の出入り方向は関係ないので黒で書きますが，すべて正値です）。カルノーサイクル $\mathsf{C}$ と $\mathsf{C'}$ は仕事が等しくなるように調整した以外は作業物質や操作については制限しておらず互いに異なるサイクルでした。しかし，以上の考察により，カルノーサイクルの個性には関係なく，カルノーサイクルが高温熱源から受け取る熱量と，低温熱源に捨てる熱量は，熱源が同じであれば等しくなるということが分かりました。カルノーサイクルが主役だと思って考察していたら，実は本質的に重要なのは熱源の性質の方でした。

前節で定義した熱機関の効率 $\eta$ を思い出しましょう。

熱機関の効率は受け入れた熱量と捨てた熱量の比に依存します。よって，カルノーサイクルの効率はカルノーサイクルの種類にかかわらず，熱源の性質のみによって決まるということになります。