熱機関

はじめにで述べたように，ジュールは熱の実体は物質そのものではなく，物質内部のミクロな運動に由来するエネルギーであることを実験的に示しました。しかし，仕事を与えて熱を取り出すのは摩擦熱などを考えてもわかるように簡単ですが，反対に熱を与えて仕事を取り出すには工夫が必要です。熱を与えて仕事を連続的に取り出すことができる装置を熱機関（heat engine）と言います。

熱と仕事が等価といっても，熱は木なり石炭なりを燃やせば手に入るので，人類は機械に仕事をさせるために，熱を仕事に変えることを望みました。

歴史的には 17 世紀末から 18 世紀初頭にかけてのイギリスでは，暖房や調理のための燃料に加え，製鉄業やガラス工業の発展による工業用途が拡大していたため，石炭の需要が急増していました。手に入りやすい地表近くの石炭は取りつくして枯渇していたので，より深部の石炭を採掘する必要があったのですが，深部では地下水が湧出するため，その排水に多くの人力や馬力がつぎ込まれていました。しかし，次第に馬の餌代が割に合わなくなり，石炭を採掘しても餌代（と人件費）に消えてしまい儲けがなくなってしまったようです。

そこで，餌を食わない機械に仕事をさせようということで発展したのが熱機関で，1712 年にニューコメン（Newcomen）が蒸気の力でポンプを動かして地下水をくみ上げる蒸気機関を発明しました。といっても，餌を食わない代わりに蒸気を発生させるために大量の石炭が必要で，採掘した石炭の多くを排水のために燃やしていたとも言われています。

なんとか蒸気機関の効率を上げて，石炭の消費を減らしたい（儲けを増やしたい）と考えるのは当然で，それに成功したのがジェームズ・ワット（James Watt）で，1769 年のことでした。

ニューコメンやワットがエンジニアとして蒸気機関の発明や改良に貢献した一方，熱機関の原理的な効率について考察し，サイエンティストとしての貢献をしたのがフランスのカルノー（Carnot）で，1824 年に発表された論文が今日の熱力学第二法則につながる重要なものであったとして高く評価されています。

熱機関の効率

熱を仕事に変えるのが熱機関ですが，第二法則を受け入れる立場であるならば，それはトムソンの原理を受け入れることと同義ですので，仕事の後には必ず何らかの影響が残ります。よって，これを定義に含めて，熱機関の一般的な定義を以下で与えることにします。

以下で熱機関の効率について考察します。初めに熱と仕事の表し方の約束について再確認しておきましょう。高校理科編 > 内部エネルギー，および本編 > 熱力学第一法則でも説明しましたが，ここまでの議論では「系」が主役で，系になされる仕事を $w$ と表し，実際に系に仕事がされれば $w > 0$，反対に系が外界に仕事をすれば，これを負の仕事がなされたとして系から見れば $w < 0$ でやはり $w$ で表し，外界から見れば $-w > 0$ の仕事がなされたとなります。また，熱についても系に入る熱量を $q$ とするので，系から熱が出たとすれば，これを負の熱量が系に与えられたとして，系から見れば $q < 0$ でやはり $q$ で表し，外界からみれば $-q >0$ の熱量が出てきたとしていました。一方，熱機関を考える際の「系」は熱機関の内部なのですが，私たちの興味はむしろ外界に与えられた仕事であったり，系に入る熱量と外界に排出された熱量の差であったりするので，上記定義は感覚的にややわかりにくいものとなってしまいます。

そこで，熱機関の議論を進めるにあたっては，系に入る仕事を $w$（今まで通り），系が外界になす仕事を $\overline{w} = -w$ として表記します。例えば $\overline{w} > 0$ の場合，熱機関は外界に正の仕事をしたことになります。熱量に関しては系に入る場合も出る場合も $q > 0$ で表し，その違いを系が「受け取る」や「捨てる」などの表現で区別することにします。（分かり易さのためとはいえ）定義を変えるのは紛らわしいので，ここでの定義の系が受け取る熱量を赤色の $\color{red}{q}$，系が捨てる熱量を青色の $\color{blue}{q}$ で表記します。色付きの $q$ は常に正の値だと思ってください。

準備が整いましたので，熱機関の効率について考えます。熱機関 $\mathsf{C}$ が高温熱源から受け取る熱量を $\color{red}{q_1}$，外界にする仕事を $\overline{w}$，低温熱源に捨てる熱量を $\color{blue}{q_2}$ とします。

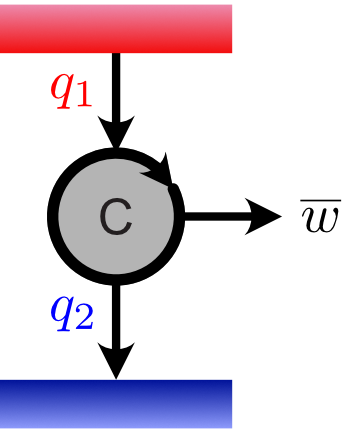
高温熱源から熱量 $\color{red}{q_1}$ を受け取り，外界に仕事 $\overline{w}$ をなして低温熱源に熱量 $\color{blue}{q_2}$ を捨てる熱機関

第一法則により，熱機関がなす仕事と熱量には $\overline{w} = \color{red}{q_1}\ \color{black}{-}\ \color{blue}{q_2}$ の関係があります。そこで熱機関の効率 $\eta$ を次式で定義します。

熱機関が受け取った熱量 $\color{red}{q_1}$ をどのくらい仕事 $\overline{w}$ に変えられたかが効率ということです。効率が $1$ に近いほど「良い熱機関」ということになりますので，捨てる熱量である $\color{blue}{q_2}$ をいかに小さくするかがポイントで，もし $\color{blue}{q_2}\ \color{black}{=0}$ とできたならば，最も効率の良い熱機関ということになります。しかし，トムソンの原理は $\color{blue}{q_2}\ \color{black}{=0}$ すなわち $\eta = 1$ で何の影響も残さずに元に戻る熱機関のサイクルは不可能と言っています。トムソンの原理は熱力学第二法則の一つの表現であり，第二法則は経験に基づいたものですので，トムソンの原理も不可能が証明されたという類のものではありません。だから「ひょっとしたら」と考える人がいるのも理解できるのですが，このような機関は第二種永久機関と呼ばれ，（少なくとも第二法則を受け入れている限りは）実現不可能な機関で，効率は決して $1$ にはなりません。それでは熱機関の効率は何によってどのように決まるのでしょうか。