内部エネルギー

速習編では内部エネルギー $U$ よりも先にエンタルピー $H$ を学ぶという暴挙に出ましたが，順番としては内部エネルギーを先に考えるのが筋なので，高校物理では内部エネルギーについて学びます。

エネルギー保存則

エネルギーの形態には，運動する物体がもつ運動エネルギー（kinetic energy）や，これまでに学んだ熱エネルギーの他，電気エネルギーや光エネルギー，そして化学エネルギー（chemical energy）などたくさん種類があります。これらのエネルギーは互いに変換することができて，例えば，摩擦で物体の運動が止まるのは，運動エネルギーが熱エネルギーに変わった結果ですし，太陽電池は光エネルギーを電気エネルギーに変換します。また，電池は化学エネルギーを電気エネルギーに変えますが，電気分解では逆に電気エネルギーを化学エネルギーに変換しているので，変換の方向は一方向ではありません。このように，エネルギーの種類は変わりうるものですが，決して変わらないものがあり，それは，これらすべてを合わせた，エネルギーの和です。

これをエネルギー保存則といいます。恐らく高校物理を履修していない方でも，何となくは知っている法則ではないでしょうか。前に熱量の保存というものを学びました。これは熱エネルギーが他のエネルギーに変換されないということを前提とした話であり，別の言い方をすると，熱量の保存はエネルギー保存の特別な場合（変換がない場合）と見ることもできます。

内部エネルギー

密閉された容器の中に入った気体を考えましょう。この気体はどのようなエネルギーを持つでしょうか。容器を車で運んでいる最中であれば，車のスピードに応じた運動エネルギーを持ちます。飛行機で運んでいる最中であれば，飛行高度で変化する，位置エネルギーを持ちます。しかし，こういうのはいかにも屁理屈っぽいので考えないことにして，容器の内部にだけ着目します。前節で学んだように，気体の分子は運動エネルギーを持ちます。また，理想気体でなければ（実在気体であれば），分子間の相互作用に関わるエネルギーがあります。分子が単原子分子でなければ，化学結合や分子の振動，回転にもエネルギーが関わります。これら一切合切をすべて合わせたエネルギーを，その気体の内部エネルギーと言い，通常 $U$ で表します。注意していただきたいのは，気体分子の運動エネルギーと気体の熱エネルギーの和をとってはいけない点です。はじめにで，「熱の実体は，構成する粒子の無秩序な動きであって，温度が上がると，この無秩序な動きが激しさを増す」と書きました。遠目で見たときに熱と思っているものをクローズアップしていくと，その実体は原子や分子の運動エネルギーということであって，両者は視点が違うだけで，実は同じものです。したがって，気体の運動エネルギーと気体の熱エネルギーの和をとると，二重カウントになってしまいます。

理想気体を考えましょう。理想気体は分子間の相互作用がない（無視できる）気体です。また，この理想気体は分子自体の回転や振動もない単原子分子であるとします。そうすると，単原子分子理想気体の内部エネルギーは，気体分子の運動エネルギーだけを考えれば良さそうです。

前節で，気体分子 1 個当たりの平均運動エネルギー $\overline{\varepsilon}$ を求めました。これを $\NA$ 倍すれば $1\unit{mol}$ 当たり，さらに $n$ 倍すれば $n\unit{mol}$ 当たりの運動エネルギーになります。したがって，単原子分子理想気体の内部エネルギーは次式で表されます。

これより，単原子分子理想気体の内部エネルギーは，絶対温度 $T$ と物質量 $n$ に比例することがわかります。エネルギー保存則より，容器の外からエネルギーが入ったり，外へ出たりしない限り，容器内のエネルギー $U$ は一定であり，外からエネルギーが入ったのであれば，入った分だけ $U$ は増え，出たのであれば，出た分だけ $U$ は減ります。

出入りするエネルギーの形態には色々ありますが，ここではこれを二つに大別します。熱としての出入りと，その他の出入りです。「その他」には例えば，電気エネルギーのようなものも含まれますが，当分そういったものは考えないので，ここでは，その他の範囲を絞り込んで，仕事（work）と限定します。

気体に限らず成り立つので，物体と書きました。これを熱力学第一法則またはエネルギー保存則といいます。熱量と仕事を表す記号として，大文字の $Q$ と $W$ を使う教科書もあります。

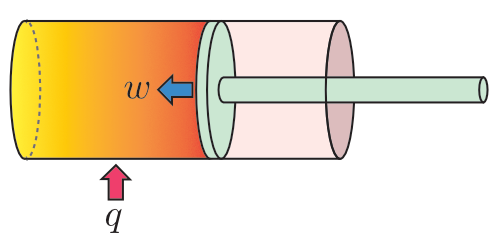
さて，気体の熱力学では，ある閉じ込められた気体に，熱量が入るか出るか，仕事が気体になされるか，あるいは気体が仕事をするか，という状況のさまざまなバリエーションを考えながら，議論を進めることになります。このシチュエーションをシンプルに表すモデルが，ピストン付きの密閉容器（シリンダー）です。容器の中に気体が入っており，外から気体を温めれば，熱量 $q$ が気体に加わります。ピストンをグイッと押して，気体を圧縮すれば，これは気体が（外からピストンを通じて）仕事をされたことになります。もし，気体が膨張して，ピストンを外に押し出せば，これは気体が（ピストンに対して）仕事をしたことになります。ここで，符号の約束をします。仕事は，前者に相当する，気体に「なされた」仕事を正であると約束します。これを $w$ と書くとき，同じだけの仕事を気体が「した」場合は，気体が負の仕事を「なされた」ということになり，$-w$ で表されます。$-w$ は $\overline{w}$ で表すこともあります。

熱量の符号についても，基本的には同じ考え方でよく，外から気体に加えられる熱量を正とし，これを $q$ で表すとき，同じだけの熱量が外に出ていく場合は，負の熱量が加えられたと考えて，$-q$ あるいは $\overline{q}$ で表します。ただし，ここからがちょっとややこしいのですが，熱量の場合，入る分も出る分も常に正で表し（つまり出る分も $q$ で表し），その方向性は符号ではなく，表現で示した方が便利な場合があります。その場合，「気体が $q_1$ の熱量を受け取り，そのうち $q_2$ を捨てたので，その差は $q_1 - q_2$ である」といった言い方をします（この場合は，$q_1$ も $q_2$ も正です）。この表現では，「捨てた」という言葉が方向性を示しています。これを，本来の言い方で表すと，「気体が $q_1$ （ただし $q_1$ は正）の熱量を受け取り，さらに $q_2$ （ただし $q_2$ は負）の熱量を受け取ったので，その和は $q_1 + q_2$ である。」となります。どちらがイメージしやすいですか？どちらの約束で話をしているのかを間違えると困ったことになりますので，頭の片隅に留めておいてください。