可逆な熱機関の効率

前節で考察したカルノーサイクルをもう少し一般化して，準静的な操作による任意の可逆な熱機関の効率を考えましょう。これは以下の図でイメージするのが分かりやすいと思います。

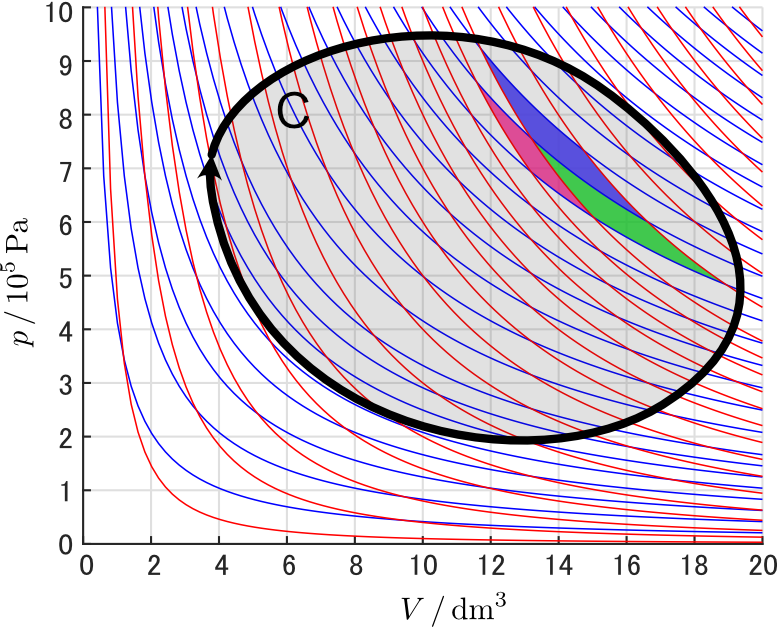
この図はすでに紹介した，条件をいろいろに変えた $1\unit{mol}$ の単原子分子理想気体の等温変化（青線）と断熱変化（赤線）の集まりの上に黒線で閉じた曲線 $\mathsf{C}$ を描いたものです。$\mathsf{C}$ の形状は任意で構いませんが，この線に沿って準静的に操作を行うとします。$\mathsf{C}$ の内側にある青線と赤線で囲まれた一つひとつの菱形のような領域はそれぞれ異なるカルノーサイクルです。

緑で塗りつぶしたカルノーサイクルに着目しましょう。このカルノーサイクルは最初の等温過程で，その上に青菱形で描かれた別のカルノーサイクルと接しています。ということは緑と青の両方のカルノーサイクルを回すと，この接した領域では青の仕事と緑の仕事，青の熱量と緑の熱量の出入りがそれぞれが相殺され，実質この境界線では何も起こらなかったのと同じことになります。同じことは緑菱形と赤菱形にも言えて，これらは断熱過程で接していますが，両者の仕事は相殺して実質なしになります（断熱なので熱の出入りはありません）。

青線と赤線は今は見やすさのため粗い分割で描いた菱形としていますが，線の間隔はいくらでも細かくすることができますので，必要なだけ細かくすれば $\mathsf{C}$ の内側を多数のカルノーサイクルできれいに埋め尽くすことができます。異なる作業物質を用いた場合でも，曲線の形状は変わりますが，$\mathsf{C}$ の内側をカルノーサイクルで埋め尽くせることには変わりありません。その場合，各カルノーサイクルどうしが接した部分での仕事や熱の授受は相殺されるのですから，結局残るのは黒線と接した $\mathsf{C}$ の外周部分のみということになります。よって，任意の準静的に操作する可逆な熱機関は同時に回すカルノーサイクルの集合体として記述できることが分かりました。

以上の議論から，カルノーサイクルに限らず，任意の準静的な操作で成立する可逆な熱機関の効率はカルノーサイクルの効率と同様，熱源の性質のみによって決まることが分かります。

これをカルノーの定理（Carnot's theorem）と言います。カルノーサイクル，あるいは任意の可逆な熱機関は理想化したものなので，実際の熱機関は可逆ではありません。以下で不可逆な熱機関の効率について考えます。

熱機関の最大効率

可逆な熱機関を準静的に操作したときの効率は熱源のみによって決まることが分かりました。では，同じ熱源を用いて可逆熱機関の効率を超える熱機関を作ることは可能でしょうか。今度は熱機関 $\mathsf{C}_\mathrm{rev}$ と熱機関 $\mathsf{C'}$ を考え，これらは熱源が同じ場合，$\mathsf{C'}$ の効率 $\eta'$ が $\mathsf{C}_\mathrm{rev}$ の効率 $\eta$ よりも優れていて，$\eta < \eta'$ だと仮定しましょう。ただし，熱機関 $\mathsf{C}_\mathrm{rev}$ は可逆とし，熱機関 $\mathsf{C'}$ は不可逆熱機関でも，あるいは $\mathsf{C}_\mathrm{rev}$ よりも効率が良い可逆熱機関でも構いません。$\mathsf{C}_\mathrm{rev}$ は高温熱源から $\color{red}{q_1}$ を受け取って仕事 $\overline{w}$ をすることができるとします。$\mathsf{C'}$ の方が効率が良い仮定なので，$\mathsf{C'}$ が高温熱源から $\color{red}{q_1}$ を受け入れてする仕事 $\overline{w'}$ は，可逆熱機関 $\mathsf{C}_\mathrm{rev}$ が同様に高温熱源から $\color{red}{q_1}$ を受け入れてする仕事 $\overline{w}$ よりも大きい（$\overline{w'} > \overline{w}$）ことになります。そこで，$\mathsf{C'}$ から取り出した仕事 $\overline{w'}$ の一部である $\overline{w}$ を $\mathsf{C}_\mathrm{rev}$ に投入することを考えます。

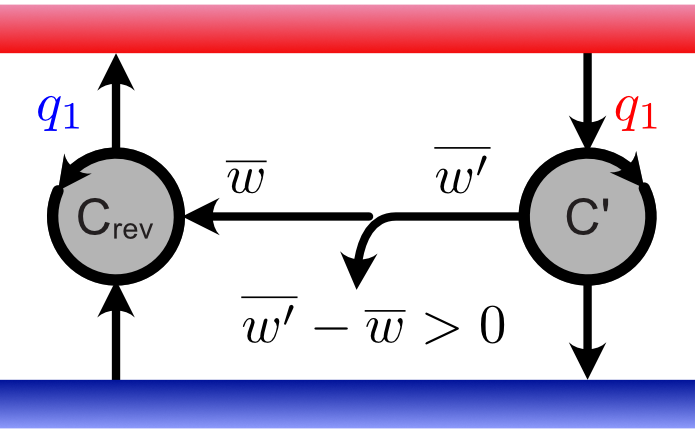
可逆熱機関 $\mathsf{C}_\mathrm{rev}$ と，より効率が良いと仮定した熱機関 $\mathsf{C'}$ との連結

$\mathsf{C'}$ は高温熱源から $\color{red}{q_1}$ を受け取り，$\mathsf{C}_\mathrm{rev}$ は高温熱源に $\color{blue}{q_1}$ を渡すので，高温熱源への正味の熱の出入りはゼロです。一方，トータルの仕事は $\overline{w'}-\overline{w} > 0$ ですので，この連結した熱機関は，低温熱源への熱の出入りの差に相当する分を，高温熱源に影響を与えることなく，仕事 $\overline{w'}-\overline{w}$ として取り出したことになります。しかしこれは「一つの熱源から熱を受け取り，他に何の影響も残さず，これをすべて仕事に変えて元の状態に戻るサイクル」の実現に他ならず，トムソンの原理に反します。

トムソンの原理に反してしまったのは，最初に可逆な熱機関 $\mathsf{C}_\mathrm{rev}$ よりも効率の良い熱機関 $\mathsf{C'}$ を仮定したからです。よって次の結果が得られます。

すなわち，ある熱源があるとき，その熱源の元で実現できる熱機関の最大の効率は可逆な熱機関の効率（これは熱源の性質によってのみ決まるが可逆な熱機関であれば同じ値をとる）であり，現実の熱機関は，原理的にこの最大効率を超えることは決してできません。