熱力学的温度

前節ではカルノーサイクル（あるいはより一般的に可逆な熱機関）の効率は，作業物質や操作の仕方には依らず，高温熱源から受け取る熱量 $\color{red}{q_1}$ と低温熱源へ捨てる熱量 $\color{blue}{q_2}$ だけに依存することを示しました（色付きの $q$ は常に正値という約束です）。熱源は系に熱を与えても受け取っても変化しないのが特徴ですので，熱源を特徴づける物理量は温度しかありません（熱源のサイズや重さなどは熱源としての性質には関係ありません）。今，私たちが知っている温度は本編 > 熱力学第 0 法則で学習した経験的温度だけですので，まずは温度計を用いて測定した熱源の経験的温度を $\theta$ を使って表すことにします。

下図のような三つの熱源と連結したカルノーサイクルを考えます。便宜上ここでは左から順に熱源 1，2，3 と呼ぶことにします。それぞれの経験的温度を温度計で測り，それらを $\theta_1$，$\theta_2$，$\theta_3$ で表します。カルノーサイクル $\mathsf{C}_1$ と $\mathsf{C}_2$ はこれまで通りです。カルノーサイクル $\mathsf{C}_3$ は $\mathsf{C}_1$ と $\mathsf{C}_2$ の二つを連結したものを一つのカルノーサイクルとみなしたものです。熱量 $\color{red}{q_1}$ を 熱源 1 より受け取り，熱量 $\color{blue}{q_3}$ を熱源 3 に捨てます。

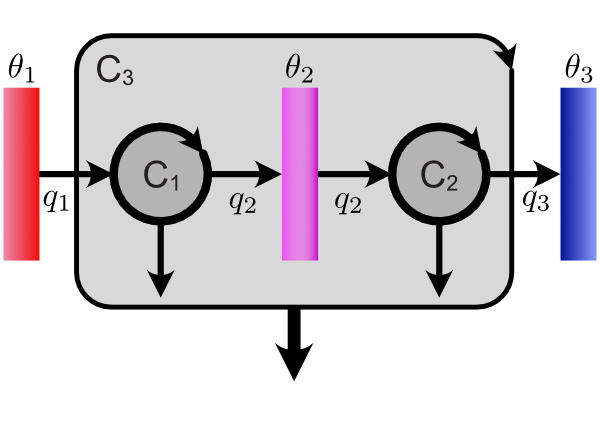
カルノーサイクルの効率は熱源の性質のみによって決まるわけですが，これらの熱源を特徴づける物理量は温度（今は経験的温度）のみです。結局 $\mathsf{C}_1$ の効率 $\eta$ は $\theta_1$ と $\theta_2$ によって決まることになるので，$\eta$ は $\theta_1$，$\theta_2$ の関数であり，$\eta\,(\theta_1,\theta_2)$ と表すことができます。今後の議論では熱量の比が重要になりますので，これを熱比 $\zeta$（ゼータ）と呼ぶことにして，$\zeta \equiv \color{red}{q_1}\color{black}{/}\color{blue}{q_2}$ と定義すると，$\zeta$ を使って $\eta$ を書いたならば，$\eta$ は熱源の温度によって決まるので，そこで使った $\zeta$ も $\theta_1$，$\theta_2$ の関数となり，$\zeta(\theta_1,\theta_2)$ と表すことができます。ここまでの流れを式にまとめます。

カルノーサイクル $\mathsf{C}_3$ は $\mathsf{C}_1$ と $\mathsf{C}_2$ を連結したものです。$\mathsf{C}_3$ の熱比は $\zeta(\theta_1,\theta_3)$ となります。すると熱比の定義より次が言えます。

式\eqref{zetaratio}の左辺には $\theta_3$ はなく，右辺にのみ $\theta_3$ があります。これは，$\theta_3$（熱源 3 の経験的温度）はどのような値であれ，この等式の成立には影響しない（右辺の $\theta_3$ が関わる部分は分母分子で相殺される）ということを意味します。$\theta_3$ に依存しないのであれば，この式の中で使う限りにおいては変数から $\theta_3$ を除くことができるので，$\zeta$ から $\theta_3$ が関わる部分を切り離して除いた新たな関数をつくり，これを $\Theta$（大文字のシータ）と呼ぶことにしましょう。$\Theta$ は経験的温度を一つだけ変数に持つ関数です。

式\eqref{zeta}の左辺は熱比であって，元となる熱源は今は経験的温度 $\theta_1$，$\theta_2$ によって特徴づけていますが，その本質は経験的温度を測るのに用いた温度計の物質に依存するものではなく，カルノーサイクルにどれだけの熱量を渡し，受け取るのかということです。すなわち 左辺の $\color{red}{q_1}\color{black}{/}\color{blue}{q_2}$ は経験的温度に関係なく定まっているものです。それが経験的温度を変数に持つ関数 $\Theta$ の比に等しいということですから，新たに $\Theta(\theta)$ を温度 $\Theta$ として定めれば，$\Theta(\theta)$ は経験的温度が変数なので，具体的にどのような関数なのかは分からない（温度計の物質に依存する）ですが，その比は物質に依存することなく定まります。このようにして定めた，用いる物質に依存せず，熱比に基づいて定めた温度 $\Theta$ を熱力学的温度（thermodynamic temperature）と言います。

式\eqref{therte}により，熱源 1，2 の熱力学的温度をそれぞれ $\Theta_1$，$\Theta_2$ とすることができます。式\eqref{therte}による定義から，熱力学的温度には下限があるということがわかります。低温熱源に捨てる熱量の最小極限は $\color{blue}{q_2}\ \color{black}{\rightarrow}\ 0$（$\color{blue}{q_2}\ \color{black}{=}\ 0$ だとトムソンの原理に反する）ですので，熱力学的温度にも極限としての最小値が存在し，この値を $\Theta = 0$ と約束します。

式\eqref{therte}は熱力学的温度の比を定めたものですので，$\Theta_1$ や $\Theta_2$ の具体的な数値はこれだけからは決まらず，比例定数の選び方により任意のスケールを取ることができます。数値を決めるには，下限の他にもう一つ基準点を定める必要があり，これは国際規約により定められます。この規約は継続的に見直されていて，科学技術の進歩に合わせて年代によって少しずつ定義が変わるのですが，2018 年までの定義では水の三重点（triple point, tp）を $273.16\unit{K}$ と定めていました。これを採用すると，低温熱源が三重点の状態にある水であるとして，ある物体の熱力学的温度 $\Theta$ は，水の三重点との熱比と比例定数である $273.16\unit{K}$ とで表すことができるようになります。

このように，$\Theta = 0$ を下限，水の三重点を $273.16\unit{K}$ に定めた上で，その間を等分割することでケルビンスケールを定義することができます。

物質に依存しない温度が定義されました。一般に熱力学では温度といえば，原則として熱力学的温度の概念を意味することになります。一方，私たちは理想気体の状態方程式により定められる絶対温度 $T$ を頻繁に用います。次節では熱力学的温度 $\Theta$ と絶対温度 $T$ の関係について考察します。