絶対温度

可逆熱機関に出入りする熱量の比によって，熱力学的温度 $\Theta$ という物質によらない温度を定義することができました。一方，私たちは理想気体の状態方程式 $pV=nRT$ を満たすための温度として，下限を $T = 0$ とし，水の三重点を $T = 273.16\unit{K}$ とする絶対温度 $T$ を用いてきました。そこで気になるのが $T$ と $\Theta$ の関係です。これまで使ってきた便利な $T$ を使って $\Theta$ をどう表せばよいのでしょうか。

この問題を考えるために，理想気体を作業物質としたカルノーサイクルの効率について考えてみましょう。カルノーサイクルの効率は作業物質に依らないので，当然，理想気体を作業物質とすることもできます。

理想気体を用いたカルノーサイクル

カルノーサイクルのプロセスを再掲します。

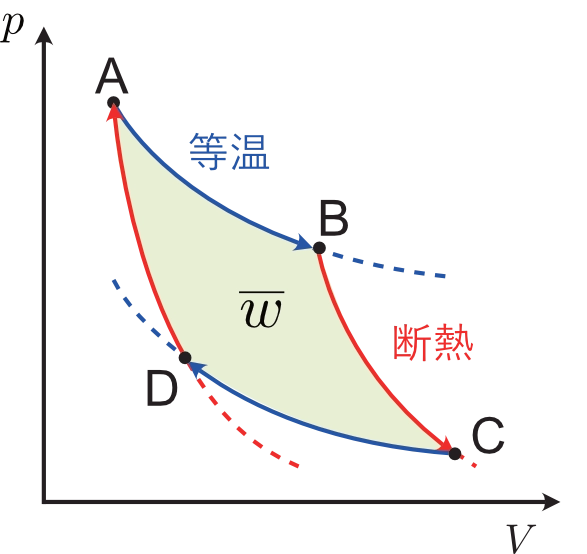
A から B の間の理想気体の絶対温度を $T_\mathrm{H}$（$T_\mathsf{A}=T_\mathsf{B}=T_\mathrm{H}$），C から D の間は $T_\mathrm{L}$（$T_\mathsf{C}=T_\mathsf{D}=T_\mathrm{L}$）とします。理想気体なので，状態方程式を用いれば，各プロセスでの仕事と熱量の出入りを計算することができます。今は系（理想気体）を主役に見ていますので，符号あり（色なし）の $q$ の定義で記述します。

AB 過程（膨張過程なので $w_\mathsf{AB} < 0$）

$$w_\mathsf{AB} = -\int_{V_\mathsf{A}}^{V_\mathsf{B}}p\,\diff V = -\int_{V_\mathsf{A}}^{V_\mathsf{B}}\frac{nRT_\mathrm{H}}{V}\diff V = -nRT_\mathrm{H}\ln\frac{V_\mathsf{B}}{V_\mathsf{A}}$$

等温過程より（理想気体なので）$\Delta U = 0$ で，第一法則より $q_\mathsf{AB} = -w_\mathsf{AB} > 0$ となります。

BC 過程（断熱過程なので $q_\mathsf{BC} = 0$）

$$w_\mathsf{BC} = \Delta U = C_V(T_\mathrm{L}-T_\mathrm{H})$$

$C_V$ は理想気体の種類によって変わりますが，（理想気体なので）温度依存性はありません。

CD 過程（圧縮過程なので $w_\mathsf{CD} > 0$）

$$w_\mathsf{CD} = -nRT_\mathrm{L}\ln\frac{V_\mathsf{D}}{V_\mathsf{C}}$$

$q_\mathsf{CD} = -w_\mathsf{CD}$ ですが，$w_\mathsf{CD}$ が正値なので，$q_\mathsf{CD}$ は負値になります。後で効率を考える際は定義に合わせて符号を変える必要があります。

DA 過程（断熱過程なので $q_\mathsf{DA} = 0$）

$$w_\mathsf{DA} = C_V(T_\mathrm{H}-T_\mathrm{L})$$

これらの結果を使って，理想気体を作業物質としたカルノーサイクルの効率を表します。

$$\eta = 1 - \frac{-q_\mathsf{CD}}{q_\mathsf{AB}} = 1 - \frac{-nRT_\mathrm{L}\ln\frac{V_\mathsf{D}}{V_\mathsf{C}}}{nRT_\mathrm{H}\ln\frac{V_\mathsf{B}}{V_\mathsf{A}}} = 1 - \frac{T_\mathrm{L}\ln\frac{V_\mathsf{C}}{V_\mathsf{D}}}{T_\mathrm{H}\ln\frac{V_\mathsf{B}}{V_\mathsf{A}}} \label{ce}$$

式\eqref{ce}中辺の分母・分子の符号に注意してください。効率は熱量を常に正で表すスタイルで定義されています。分母は仕事 $w_\mathsf{AB}$ の符号を反転させたものが正値なので，マイナス記号は付きません。分子は上で求めた $q_\mathsf{CD}$ が負値なので，これを正値に変換するためにマイナス記号を付けますが，仕事 $w_\mathsf{CD}$（もともとマイナスが付いている）のマイナスのマイナスなので，結果的にマイナス記号が付きます。右辺では分子の自然対数の中を逆数にしたため，マイナスが取れます。

ここで本編 > 理想気体の断熱変化の内容を思い出すと，以下の関係が導かれます。

\begin{align} &\frac{T_\mathsf{B}}{T_\mathsf{C}} = \frac{T_\mathrm{H}}{T_\mathrm{L}} = \left(\frac{V_\mathsf{C}}{V_\mathsf{B}}\right)^{1/c}\\[3ex] &\frac{T_\mathsf{D}}{T_\mathsf{A}} = \frac{T_\mathrm{L}}{T_\mathrm{H}} = \left(\frac{V_\mathsf{A}}{V_\mathsf{D}}\right)^{1/c}\\[3ex] &\Rightarrow \frac{T_\mathsf{A}}{T_\mathsf{D}} = \frac{T_\mathrm{H}}{T_\mathrm{L}} = \left(\frac{V_\mathsf{D}}{V_\mathsf{A}}\right)^{1/c} \Rightarrow \frac{V_\mathsf{C}}{V_\mathsf{B}} = \frac{V_\mathsf{D}}{V_\mathsf{A}} \Rightarrow \frac{V_\mathsf{B}}{V_\mathsf{A}} = \frac{V_\mathsf{C}}{V_\mathsf{D}}\label{bacd} \end{align}

式\eqref{bacd}の関係を用いることで，理想気体を作業物質としたカルノーサイクルの効率は次のように整理できます。

$$\eta = 1 - \frac{\Theta_\mathrm{L}}{\Theta_\mathrm{H}} = 1 - \frac{T_\mathrm{L}}{T_\mathrm{H}} \label{etaabs}$$

熱機関の効率は熱量の比を元にした熱力学的温度 $\Theta$ で定義されるものですが，理想気体を作業物質に用いた場合，$q$ を具体的に計算して効率を絶対温度 $T$ で表すと，$\Theta$ の比と $T$ の比が一致することが確認できます。後は具体的な数値を決めるための比例係数が必要ですが，既に述べたように，熱力学的温度と絶対温度のいずれの場合も最小値をゼロ，水の三重点を $273.16\unit{K}$ と共通の基準を採用しています。結果として絶対温度と熱力学的温度は，出発点となる考え方は異なりますが，実際には数値的に等価な温度として扱うことができます。よってこれ以降も，温度としてこれまで通り（理論的お墨付きを与えられた）絶対温度を議論に用いることとし，これをこれまで通り記号 $T$ で表します。