熱力学第二法則

高校物理では熱力学第二法則にも簡単ながら言及があります。熱力学第二法則を言葉で表現するには色々な方法があるのですが，以下はその一つで，クラウジウス（Clausius）の原理と呼ばれています。

要するに，「熱は熱い方から冷たい方に移動する」という，方向性を示した法則です。ただし，「仕事を熱に変えることなしに」という条件が付いているので，逆に言えば，仕事を熱に変えたならば，熱を冷たい方から熱い方へ移すこともできるということです。他の表現方法には次のようなものもあって，こちらはトムソン（ケルビン）の原理と呼ばれています。

熱機関の $P$-$V$ 図

下の $P$-$V$ 図に示すように，気体がある状態 A からスタートして，圧力と体積が変わりながら（そうなるように熱量を調節して），状態 B を経て，そこから，コンディションが変わって（$P$-$V$ 図上の道筋が変わって），状態 C にたどり着いたとします。ここまでは体積 $V$ が増加する過程ですので，気体は外に仕事をしています。さて，今度は状態 C から，状態 D を経て，再び状態 A に戻ることを考えましょう。体積と圧力だけを見れば，完全に元の状態に戻ったように見えますが（当然，温度も戻ります），一周する間に熱や仕事の出入りがありますので，容器の外の世界も含めたすべてが元通りということではありません。

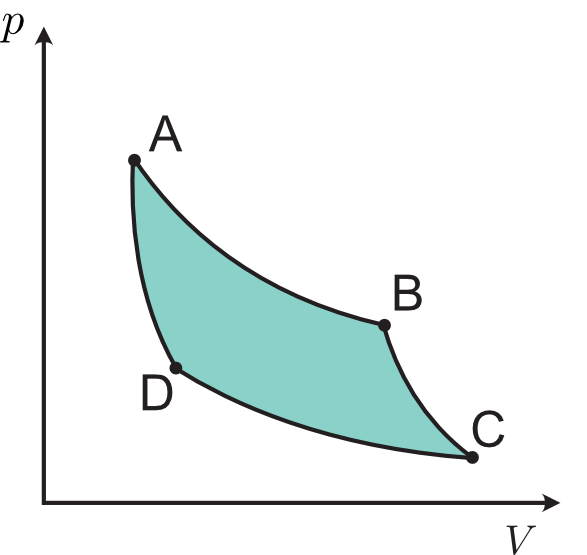
熱機関の $P$-$V$ 図

グルッと一周したときに，トータルで気体が外に対してなした仕事は，前節で学んだ積分の応用で求めることができます。つまり，A $\rightarrow$ C までの積分で得られる面積から，C $\rightarrow$ A までの面積を引いてあげれば（実際は積分範囲が右から左なので，足し算になります），気体が外に対してなした仕事が求まります。これは下図で色付けして囲まれた部分の面積を求めることに相当します。〇はグルっと一周の意味です。

このようなサイクルを回すには，熱の出し入れが必要です。一般に，高温の熱源から熱を受け取り，その一部を仕事に変えて，残りを低温の熱源に捨てる装置を熱機関といいます。代表例は蒸気機関です。当然ながら，気体には仕事をしてもらいつつも，無駄となる，捨てる熱をできるだけ減らしたい。熱機関が高温熱源から受け取る熱量を $q_1$，低温熱源へ捨てる熱量を $q_2$ とすると，グルっとまわって同じ温度に戻るのであれば，熱力学第一法則より，熱機関がなす仕事 $\overline{w}$ は熱量の差と一致し，$\overline{w} = q_1 − q_2$ となります。そこで，熱機関の効率 $\eta$（イータ）を以下で定義することにします。

理想は捨てる熱 $q_2$ をゼロにして，効率 $\eta$ を $1$ にすることです。しかしトムソンの原理は，$\eta = 1$ で，何も影響を残さずに元の状態に戻るサイクルをもつ熱機関を作ることは不可能であるということを述べています。このような機関を第二種永久機関といい，なんとなくできそうなので，多くの先人たちが，これを実現しようとして夢敗れています。これは速習編で「バラバラの運動から秩序ある運動を取り出すのはどう考えても分が悪く」と説明したことに対応しており，エントロピーの議論につながる大切な部分です。

さて，これで高校理科における熱の取り扱いを駆け足で復習することができました。