還元電位と熱力学

講義 > 酸・塩基 > 熱力学的な解釈でブレンステッド酸の $\pKa{}$ の大小の要因を熱力学に基づいて考察しました。本節では標準還元電位 $\Eo$ の大小について熱力学的な観点から考察します。

金属の酸への溶解反応

$\Eo$ は標準水素電極 SHE を基準とするので，金属 $\ce{M(s)}$ が酸に溶けて $\ce{M+(aq)}$ と $\ce{H2}$ が生成する反応をモデルとします。このとき $\Eo$ の大小を考えるにはギブズエネルギー変化を考えるのが本来ですが，簡単のためエントロピーの効果は無視してエンタルピー変化に着目します。下図を見ながら説明を読み進めてください。

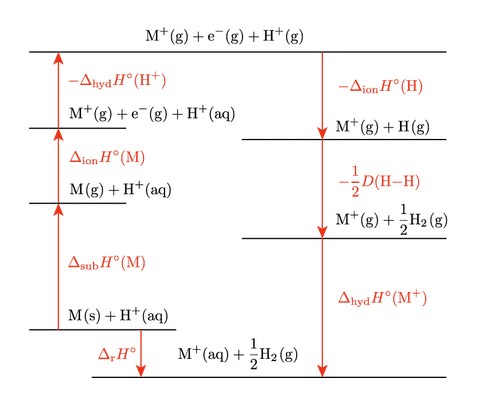
金属の酸への溶解のエネルギーダイヤグラム

固体の金属 $\ce{M(s)}$ と水和したプロトン $\ce{H+(aq)}$ を起点とし，ゴールは水和した金属イオン $\ce{M+(aq)}$ と気体の水素 $\ce{H2(g)}$ です。このときのエンタルピー変化（金属の酸への溶解のエンタルピー変化）をここでは $\DHo{r}$ とします。図で言うと一番下とそのすぐ上の横線の間隔に相当します。この間隔の大きさに影響を与える要因を考察するというのが今やりたいことであり，そのために回り道して考えます。最初は $\ce{M(s)}$ を気体にします。昇華エンタルピー $\DHo{sub}$ 分のエネルギーが必要です。もし単体金属以外の物質であれば原子化エンタルピー $\DHo{at}$ を考えることになります。次に気体の金属原子をイオン化します。イオン化エンタルピー $\DHo{ion}$ 分のエネルギーが必要です。そして次はプロトンの水和水を引きはがして気相のプロトン $\ce{H+(g)}$ にします。水和するときのエンタルピー変化が水和エンタルピー $\DHo{hyd}$ であり，ここではその反対の引きはがしですのでマイナス符号が付いた $-\DHo{hyd}$ 分のエネルギーが必要です。これで図の一番上の状態になりました。

次は一番上から下ります。初めはプロトンに電子を渡します。これをプロトンの電子獲得エンタルピーとしても良いですが，水素原子のイオン化の逆ですので $-\DHo{ion}$ で表します。生じた水素原子を水素分子にします。$\ce{H2}$ の結合解離エネルギーの反対符号です。最後に気相の金属イオンを水和してゴールである図の一番下にたどり着きます。金属の違いによる $\Eo$ の違いを考えるときは水素に関わる部分は共通しますので，着目するポイントは $\DHo{sub}(\ce{M})$，$\DHo{ion}(\ce{M})$，$\DHo{hyd}(\ce{M+})$ の三つとなります。

アルカリ金属元素の標準電極電位

アルカリ金属元素の標準電極電位（$25\oC$，$1\unit{atm}$）を示します。

Reaction	$\Eo /\unit{V}$
$\ce{Na+ + e- <=> Na}$	$-2.71$
$\ce{K+ + e- <=> K}$	$-2.931$
$\ce{Rb+ + e- <=> Rb}$	$-2.98$
$\ce{Cs+ + e- <=> Cs}$	$-3.026$
$\ce{Li+ + e- <=> Li}$	$-3.0401$

これを見ると電極電位は周期表の並びとは違っています。といっても $\ce{Na+}$ がこの中では一番還元されやすく $\ce{Cs+}$ までは周期表の族の順になっていますので，例外は $\ce{Li+}$ です。$\ce{Li+}$ が還元されにくくなる要因は何でしょうか。アルカリ金属元素の熱力学パラメータを比べてみましょう。エンタルピー変化の単位は $\mathrm{kJ\,mol^{-1}}$ です。

	$\DHo{sub}(\ce{M})$	$\DHo{ion}(\ce{M})$	$\DHo{hyd}(\ce{M+})$	$\DHo{f}(\ce{M+,aq})$
$\ce{Li}$	$159.3$	$680$	$-1117.8$	$-278.5$
$\ce{Na}$	$107.5$	$603$	$-950.6$	$-240.1$
$\ce{K}$	$89.0$	$508$	$-849.4$	$-252.4$
$\ce{Rb}$	$80.9$	$484$	$-816.1$	$-251.2$
$\ce{Cs}$	$76.5$	$452$	$-786.8$	$-258.3$

イオンの標準生成エンタルピーはプロトンの標準生成エンタルピーをゼロと定義してこれを基準とした相対値を用いることになっていますので，表中の $\DHo{f}(\ce{M+,aq})$ は上図の $\DHo{r}$ に対応します。これを見るとたしかに $\ce{Li}$ は他の元素と比べて $\DHo{f}(\ce{M+,aq})$ が負に大きい（カチオンになりやすい = 還元しにくい）ことが分かります。$\DHo{f}(\ce{M+,aq})$ は昇華エンタルピー $\DHo{sub}$，イオン化エンタルピー $\DHo{ion}$，イオンの水和エンタルピー $\DHo{hyd}(\ce{M+})$ を足し合わせたものです。表を見ると $\ce{Li}$ の水和エンタルピーが目立って負に大きいことがわかります。これはイオン半径が小さいイオンでは正電荷の密度が高いため，水和による安定化の効果が大きく表れるためです。つまり $\DHo{sub}$ と $\DHo{ion}$ が高周期元素になるにつれて小さくなる効果を打ち消すくらいに $\ce{Li}$ の $\DHo{hyd}(\ce{M+})$ が負に大きいために順番が逆転して $\ce{Li}$ の $\DHo{f}(\ce{M+,aq})$ が負に大きい（還元しにくい = $\Eo$ が負に大きい）という結果になっているわけです。

イオン半径の違いが $\DHo{hyd}(\ce{M+})$ を通じて $\Eo$ に影響を与えていることが分かりました。ではイオン半径が近いイオンどうしの比較ではどうでしょうか。ナトリウムイオン $\ce{Na+}$ と銀イオン $\ce{Ag+}$ はイオン半径が比較的近いので比較してみましょう。

Reaction	$\Eo /\unit{V}$
$\ce{Ag+ + e- <=> Ag}$	$0.7996$
$\ce{Na+ + e- <=> Na}$	$-2.71$

	$\DHo{sub}(\ce{M})$	$\DHo{ion}(\ce{M})$	$\DHo{hyd}(\ce{M+})$	$\DHo{f}(\ce{M+,aq})$
$\ce{Na}$	$107.5$	$603$	$-950.6$	$-240.1$
$\ce{Ag}$	$284.9$	$1016$	$-1195.3$	$105.6$

今回は $\ce{Ag}$ の $\DHo{ion}(\ce{M})$ が $\ce{Na}$ と比べて目立って大きくなっておりこれが $\Eo$ の違いの主要因であることがわかります。これは（イオンのサイズが近いにもかかわらず）原子番号が大きい $\ce{Ag}$ の核電荷が大きく，かつ $\ce{Ag}$ の $\ao{4d}$ 電子は遮蔽効果が小さいため，$\ce{Na}$ と比べて $\ce{Ag}$ は価電子が強く束縛されているためです。