熱力学的な解釈

前節ではブレンステッド酸の強さを酸解離定数 $\Ka{}$ あるいは $\pKa{}$ で表すことを学びました。しかし，そもそもどのようなときに酸は強くなるのか，酸の強さの理由については $\pKa{}$ は答えてくれません。本節では，熱力学の立場から，酸が強くなる要因について考察します。熱力学の用語や考え方をいくつか使いますので，不慣れな方は講義 > 化学熱力学を参照してください。

気相における酸の強さ

簡単のため，はじめにブレンステッド酸 $\ce{HA}$ が気相，すなわち溶媒分子に囲まれていない場合を考えます。$\ce{HA}$ が強い酸であるほど，共役塩基である $\ce{A-}$ は弱い塩基になりますので，次の反応を考えます。

$$\ce{A-(g) + H+(g) <=> HA(g)}$$

$\ce{A-}$ が強い塩基であるとき，この反応は大きく右に寄る，すなわち平衡定数 $K_P^\circ$ が大きくなります。講義 > 化学熱力学：速習編で学習したように，これはギブズエネルギー変化 $\DGo{pg}$ が負に大きいことに対応します。ここで，$\mathrm{pg}$ は proton gain の意味です。したがって，$\DGo{pg}$ の大きさを変化させる要因を考えれば，ブレンステッド酸の強さを熱力学的に理解したことになります。今は反応物も生成物も気体を想定していますので，反応の前後でのエントロピー変化は小さいと考えられます。そこで，簡単のため $\DGo{pg} \approx \DHo{pg}$ と考えることにしましょう。下図を見ながら説明を読み進めてください。

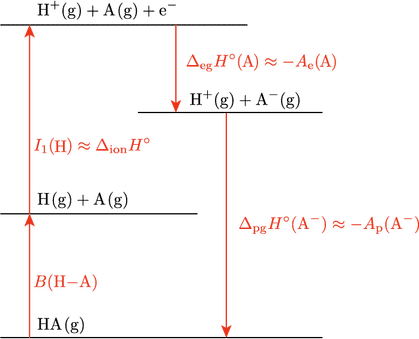
HA解離のエネルギーダイヤグラム

知りたいのは $\DHo{pg}(\ce{A-})$ ですが，図の一番下の $\ce{HA(g)}$ から順を追って考えます。はじめに，$\ce{HA(g)}$ の結合が解離して水素原子 $\ce{H(g)}$ と $\ce{A(g)}$ が生じる過程を考えると，必要なエネルギーは結合の解離エネルギー $B(\ce{H-A})$ です。次に，水素原子が電子を放出してプロトンとなる過程を考えますが，これに必要なエネルギーは水素原子の第一イオン化エネルギー $I_1(\ce{H})$ です。ここまでが上図の左に示した上向き矢印の過程になります。次に $\ce{A(g)}$ が電子を受け取って $\ce{A-(g)}$ となりますが，このときのエンタルピー変化が電子獲得エンタルピー $\DHo{eg}(\ce{A})$ です。これで目的の $\ce{H+(g)}$ と $\ce{A-(g)}$ が得られました。$\ce{H+(g)}$ と $\ce{A-(g)}$ から $\ce{HA(g)}$ が生じる過程のエンタルピー変化が $\DHo{pg}$ ですので，$\DHo{pg}$ の大きさは $B(\ce{H-A})$，$I_1(\ce{H})$，$\DHo{eg}(\ce{A})$ に依存することがわかります。

$$B(\ce{H-A}) + I_1(\ce{H}) + \DHo{eg}(\ce{A}) + \DHo{pg}(\ce{A-}) = 0 \label{BHAI1}$$

エンタルピーで議論を続けても構いませんが，使い慣れた用語の電子親和力（electron affinity）$\Ae$ に置き換えましょう。エンタルピーとは符号が反転する約束です。それから，同様の考えで，プロトン親和力（proton affinity）$\Ap$ も導入します。式(\ref{BHAI1})は次のように書き換えられます。

$$\Ap(\ce{A-}) = B(\ce{H-A}) + I_1(\ce{H}) - \Ae(\ce{A}) \label{ApBIAe}$$

さて，$I_1(\ce{H})$ は固定なので，$\Ap(\ce{A-})$ が影響を受ける要因が，$B(\ce{H-A})$ と $\Ae(\ce{A})$ であることが分かりました。周期表の同周期元素を考えてみましょう。例えば，第 2 周期の $\ce{NH3}$，$\ce{H2O}$，$\ce{HF}$，第 3 周期の $\ce{H2S}$，$\ce{HCl}$ を見て分かるように，同周期であれば，周期表で右に行くほど $\pKa{}$ は小さく，強いブレンステッド酸になります。そのカギを握るのは電子親和力 $\Ae$ です。周期表で右に行くほど元素は陰性で $\Ae$ が大きくなります。したがって，式(\ref{ApBIAe})より，$\Ap$ は小さくなる，すなわち，$\ce{A-}$ がプロトンを受け取ったときの安定化が小さくなります。これは $\ce{A-}$ が弱い塩基になることを意味しますので，周期表で右に行くほど，ブレンステッド酸 $\ce{HA}$ の $\pKa{}$ は小さくなります。

では次に，同族元素はどうでしょうか。ハロゲン化水素が分かりやすくて，$\pKa{}$ は高周期になるほど小さくなります。ここでのカギは結合の解離エネルギー $B(\ce{H-A})$ です。高周期元素ほど結合は弱く，$B(\ce{H-A})$ が小さくなりますので，その結果，$\Ap$ は小さくなってブレンステッド酸 $\ce{HA}$ の $\pKa{}$ は小さくなります。このように，周期で見るか，族で見るかによって，ブレンステッド酸の強さを決める主役となる因子は異なっていることが熱力学的な考察からわかります。

溶媒の効果

これまでは気相での反応を考えてきました。しかし溶媒が存在すると，プロトンは溶媒和により安定化します。水溶液であれば，水和によってプロトン表面の高密度の正電荷がやわらぎ，安定化します。この溶媒和の効果を含めたプロトン親和力を，有効プロトン親和力（effective proton affinity）と呼び，$\Apeff$ で表します。

$$\ce{HA(aq) + H2O(l) <=> H3O+(aq) + A-(aq)} \label{HAH2OH3OA}$$

反応(\ref{HAH2OH3OA})において，$\Apeff(\ce{A-})$ が $\Apeff(\ce{H2O})=1130 \kJmol$ と比べて小さいとき，$\ce{HA}$ はプロトンを離しやすいので，反応(\ref{HAH2OH3OA})は平衡が右に傾きます。

$$\ce{A-(aq) + H2O(l) <=> HA(aq) + OH-(aq)} \label{AH2OHAOH}$$

反応(\ref{AH2OHAOH})において，$\Apeff(\ce{A-})$ が $\Apeff(\ce{OH-})=1188 \kJmol$ と比べて大きいとき，$\ce{A-}$ はプロトンを受け取りやすいので，反応(\ref{AH2OHAOH})は平衡が右に傾きます。

溶媒和がエントロピーに与える影響は無視できないため，溶媒中の議論ではギブズエネルギー変化 $\DGo{}$ を用いましょう。溶媒和によるギブズエネルギー変化はボルンの式（Born equation）により見積もることができます。

$$\DGo{solv} = -\frac{\NA z^2e^2}{8\pi \varepsilon_0 r}\left(1-\frac{1}{\varepsilon_\mathrm{r}}\right) \label{Borneq}$$

$\ce{HA}$ の共役塩基である $\ce{A-}$ が溶媒和によって安定化されると，$\ce{HA}$ の酸性が強くなりますが，式(\ref{Borneq})は，$\frac{z^2}{r}$ が大きいほど溶媒和による安定化が大きくなることを示しています。すなわち，電荷 $z$ が高電荷で，サイズ $r$ が小さいイオンほど大きく安定化され，また比誘電率 $\varepsilon_\mathrm{r}$ が大きいほど，大きく安定化されることになります。なお，水は $\varepsilon_\mathrm{r} = 80$ と，比誘電率がとても大きな溶媒です。

塩基 $\ce{NH3}$ の共役酸 $\ce{NH4+}$ は電荷を持ち，溶媒和による安定化を受けるため，$\ce{NH4+}$ はプロトンを離しにくく，弱い酸性を示します。特に水溶媒では，水素結合の影響により，ボルンの式で予測される以上の安定化がみられる傾向があります。