ラカーパラメータ

本節からは錯体の吸収スペクトルのうち，特に $\ao{d}$-$\ao{d}$ 遷移に着目し，実験で観測される吸収帯が理論的にはどのように理解できるのかについて考えます。錯体の配位構造には六配位正八面体や四配位正四面体などのいくつかの基本形がありますが，実際の錯体は同じ配位構造であっても配位子が異なれば，異なる吸収スペクトルの形状を示します。これは配位子の違いによって結晶場（配位子場）の強さが異なるためですが，これを経験的にまとめて並べたのが既に学んだ分光化学系列です。しかし，できることなら経験的にではなく，より理論に立脚して配位子の違いによるスペクトル形状の違いを理解したいと考えるのが自然な流れです。

電子間の反発等を考慮して，結晶場の詳しい計算を行うと，その結果は結晶場の対称性，すなわち形に基づく部分と，サイズに基づく部分に分離することができ，前者の対称性に基づく部分は，実は配位子の種類によらず，結晶場の対称性と $\ao{d}$ 電子の数さえ同じであれば同じ結果が得られます。もう少し具体的に言うと，例えば $\ao{3d}$ 軌道に対する結晶場を考えたときに，角度方向の座標成分しか持たない球関数に由来する部分は，結晶場の対称性さえ同じであれば配位子の種類によらず同じ結果が得られます。これは逆に言うと，動径関数に基づく部分は配位子の種類に応じて変わるので，この部分を配位子の違いを反映するように評価してあげることで，配位子の違いによるスペクトル形状の違いを理論的に理解することが可能です。

詳しい計算過程はここでは示しませんが，$\grp{O}{h}$ 型結晶場では上で述べた配位子の違いを表すために必要な独立なパラメータは全部で三つであることが分かっていて，これを $A$，$B$，$C$ の三つで表したものをラカーパラメータ（Racah parameters）と呼んでいます。教科書によっては $F_0$，$F_2$，$F_4$（あるいは $F^0$，$F^2$，$F^4$）の表記で書かれるパラメータを紹介しているものもあると思いますが，こちらはスレーター・コンドンパラメータ（Slater-Condon parameters）と呼ばれるものです。両者は定義が少し異なるのですが，互いに変換可能ですので，ここでは後の説明に便利なラカーパラメータで話を進めることにします。

オーゲル図

自由イオン（弱い結晶場の極限）の原子項からスタートして，結晶場を強くしていったときに，原子項がどのように分裂してそのエネルギーが変化していくかを図に表したものをオーゲル図（Orgel diagram）といいます。下に $\grp{O}{h}$ 結晶場における $\ao{d}^1$ 電子配置のオーゲル図を示します。$\ao{d}$ 軌道が $\grp{O}{h}$ 型の結晶場によって $\irrep{t}{2g}$ 軌道と $\irrep{e}{g}$ 軌道に分裂するときの図と似ていますが，ここで描いているのは軌道ではなく，状態のエネルギーですので注意してください。

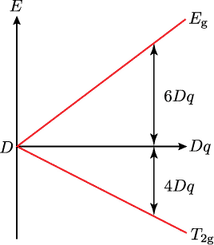
$\ao{d^1}$ の Orgel 図

図の一番左は結晶場がゼロの状態で，原子項 $D$ が基準となります。縦軸はエネルギー，横軸は結晶場の強さを $Dq$ 単位で表していて，右に行くほど強い結晶場となります。原子項 $D$ からスタートして，結晶場を強くしていくと，状態が基底状態の $\irrep{T}{2g}$ 項と励起状態の $\irrep{E}{g}$ 項に分裂し，その分裂幅が $10Dq$ であることが示されています。もちろんこれも立派なオーゲル図なのですが，これだけではあまり有難い感じがしませんので，もう少し実用的なオーゲル図にグレードアップしましょう。実は $\ao{d}^1$ 電子配置と $\ao{d}^6\mathrm{(HS)}$ 電子配置はどちらも基底項が $D$ で，$\grp{O}{h}$ 型結晶場に対して同じ分裂をしますので，これを下図の右側半分のようにまとめて描いてしまいます（といっても $\ao{d}^1$，$\ao{d}^6\mathrm{(HS)}$ を書き足しただけです）。

さらに，$\ao{d}^4\mathrm{(HS)}$ と $\ao{d}^9$ は，やはり原子項が $D$ で $\irrep{T}{2g}$ 項と $\irrep{E}{g}$ 項の上下が入れ替わった形となりますので，これを図の左側半分に描いて，四つの電子配置のオーゲル図を一枚の図としてまとめてしまいましょう。このように左右入れ替わりの関係になるのは，半閉殻の $\ao{d}^5$ 電子配置を超える電子数の場合，電子が増えていくと見る代わりに，$\ao{d}^{10}$ を基準として，電子が減るとホール（正電荷）が増えていくと考えると，正負の差があるので上下の反転はあれど，結晶場との関係性という意味では両者は等価であるためです。つまり $\ao{d}^1$ と $\ao{d}^9$ および $\ao{d}^6\mathrm{(HS)}$ と $\ao{d}^4\mathrm{(HS)}$ はそれぞれペア（相補的関係）となります。

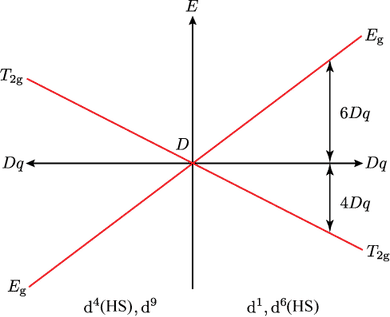
$D$ 項の Orgel 図

今は基底状態が $D$ 項の電子配置についてまとめました。他の電子配置についても見てみましょう。下図は基底状態が $F$ 項のオーゲル図で，$\ao{d}^2$，$\ao{d}^7\mathrm{(HS)}$ および $\ao{d}^3$，$\ao{d}^8$ 電子配置がこれに該当します。

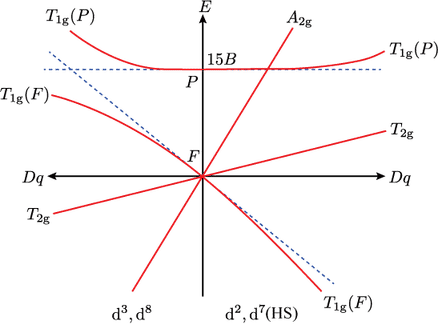
$F$ 項の Orgel 図

先ほどとはいくつかの点で異なっています。一つは基底項 $F$ の上に $P$ 項があり，そのエネルギーが $15B$ とあります。この $B$ は上述したラカーパラメータの一つで，基底状態を基準とすると，自由イオンの状態ではそこから $15B$ だけエネルギーが高いところに励起状態である $P$ 項があるということを示しています。ラカーパラメータには他に $A$ と $C$ がありますが，励起状態と基底状態のエネルギー差をとると，ここでは $B$ だけが残ります。

二つ目の特徴は，基底項 $F$ は結晶場によって $\irrep{A}{2g}$，$\irrep{T}{2g}$，$\irrep{T}{1g}$ 項の三つに分裂し，$\ao{d}$ 原子軌道の結晶場分裂の図とはずいぶんと異なる形状を示すということです。しかし上でも注意したように，ここで示しているのは軌道ではなく状態のエネルギーですので，これは不思議でもなんでもありません。もし $\ao{f}$ 原子軌道に $\grp{O}{h}$ 型の結晶場をかければ，軌道エネルギーはこのように分裂します。一方，$P$ 項は分裂していません。つまり，$\ao{p}$ 原子軌道に $\grp{O}{h}$ 型の結晶場を与えたとしても，縮退はとけません。結晶場分裂が $\ao{d}$ 電子をもつ遷移金属錯体で重要になる理由がここからもお分かりいただけるかと思います。

そして三つ目ですが，よく見ると $\irrep{T}{1g}$ 項は二つあって，$P$ 項由来の $\irrep{T}{1g}(P)$ と $F$ 項由来の $\irrep{T}{1g}(F)$ があります。そして更に，$Dq$ の増加に伴う $\irrep{T}{1g}$ 項のエネルギー変化は直線的ではなく，カーブを描いています（青の破線は直線を仮定した補助線です）。実は $\irrep{T}{1g}$ 項が二つあるのがカーブを描く理由で，このように違う項由来で生じた同じ対称性を持つ項同士は互いに相互作用し，お互いのエネルギーが離れていく（エネルギーが高い方はより高く，低い方はより低くなる）という現象があり，これを配置間相互作用（configuration interaction, CI）といいます。

$F$ 項と $P$ 項以外にはないの？あるいは上の場合であれば $D$ 項しかないの？と疑問に思うかもしれませんが，オーゲル図を描く際には，基底状態とスピン多重度が等しい励起状態のみを描くのが一般的です。$\ao{d}^1$ と $\ao{d}^9$ はそもそも $D$ 項しかありませんし，$\ao{d}^6\mathrm{(HS)}$ と $\ao{d}^4\mathrm{(HS)}$ は基底状態のスピン多重度である $2S+1 = 5$（五重項）と同じスピン多重度を持つ励起状態はありません。また，下の場合では $F$ 項と同じスピン多重度を持つ励起状態は $P$ 項のみです。

オーゲル図は高スピン状態のみを考えるのが一般的ですが，それでも上の二つのオーゲル図ではすべての電子配置をカバーしきれていません。$\ao{d}^0$ と $\ao{d}^{10}$ は除いたとしても，$\ao{d}^5\mathrm{(HS)}$ がないのは何故でしょう。$\ao{d}^5\mathrm{(HS)}$ の基底状態は $\irrep{^6S}{}$ で，他に六重項の励起状態はありません。また $S$ 項は（軌道角運動量に関して）縮退していないので，結晶場によって分裂することもありません。ということでスピン多重度が等しい励起状態も結晶場分裂もないので，オーゲル図をつくるメリットがなく，図として用意されていないというのがその理由です