エントロピー

熱力学第二法則を受け入れるならば，カルノーサイクル（より一般には可逆な熱機関）の効率は熱源の熱比のみによって決まり，熱比をもって熱力学的温度を定義することができるということがこれまでの議論で示されました（実際には熱力学的温度は絶対温度と数値的にイコールなので，これまで通り絶対温度を今後も使います）。言わばカルノーサイクルの効率が第二法則を特徴づけているということになります。

一方，熱力学第一法則での議論を振り返ると，第一法則はエネルギー保存則であり，内部エネルギー $U$ が系を特徴づける状態量として重要な役割を果たします。第二法則には系を特徴づける状態量はないのでしょうか。これまでの議論では，熱源は状態量である温度で特徴づけられていますが，系である熱機関そのものは，状態量ではない仕事と熱によって記述してきました。もちろん，内部エネルギー $U$，体積 $V$，圧力 $p$，温度 $T$ はサイクルを ABCDA と一周したときに元に戻るので変化量がゼロになる状態量ですが，これらによっては第二法則の本質である「効率の最大値」や「熱の移動方向の制限」を特徴づけることはできません。

カルノーサイクルの効率 $\eta$ を改めて確認してみます。今はカルノーサイクルを主役で見ていますので，符号あり（色なし）の $q$ を用いることにし，そのため捨てる $q_\mathsf{CD}$ は負値となるので，（$\eta$ の定義と合わせるため）$q_\mathsf{CD}$ にマイナス記号がついています。

\begin{align} &\eta = 1 - \frac{-q_\mathsf{CD}}{q_\mathsf{AB}} = 1 - \frac{T_\mathrm{L}}{T_\mathrm{H}} \label{reveta}\\[3ex] &\Rightarrow\quad \frac{-q_\mathsf{CD}}{q_\mathsf{AB}} = \frac{T_\mathrm{L}}{T_\mathrm{H}} \label{qqTT} \end{align}

この熱比の関係は，準静的な等温過程における理想気体の性質とカルノーサイクルの可逆性に基づいたものでした。式\eqref{qqTT}は以下のように変形すると，とても含蓄のあるものになります。

$$\frac{-q_\mathsf{CD}}{T_\mathrm{L}} = \frac{q_\mathsf{AB}}{T_\mathrm{H}} \quad\Rightarrow\quad \frac{q_\mathsf{AB}}{T_\mathrm{H}} + \frac{q_\mathsf{CD}}{T_\mathrm{L}} = 0 \label{qTqT}$$

断熱過程での熱の出入り（$q_\mathsf{BC}$ と $q_\mathsf{DA}$）はゼロですので，式\eqref{qTqT}の意味するところは，カルノーサイクルを一周したとき，各過程での系に入る熱量（今は $\mathsf{AB}$ 過程と $\mathsf{CD}$ 過程）をそれぞれの過程での温度で割った値の和はゼロになるということです。

すでに議論したように，任意の可逆な熱機関は小さなカルノーサイクルの集合体で表せます。これらの微小カルノーサイクルの向かい合って相殺しない部分の熱の出入りを $\delta q_\mathrm{rev}$ で書くことにすると，これらを一周足し合わせたものもゼロとなります。

$$\oint\frac{\delta q_\mathrm{rev}}{T} = 0$$

一周して始状態と同じ状態に戻るまでの積分が（可逆ならば）経路にかかわらずゼロになるということは，微小量の熱の出入り $\delta q_\mathrm{rev}$ ごとに系のある物理量が変化し，サイクルを一周した終状態では元の物理量に戻る，すなわち一周全体での変化量がゼロということになります。これはサイクルをどう回したかという経路に依らないので，どうやら新しい状態量の有力候補が見つかったようです。これをエントロピー（entropy）と呼ぶことにしましょう。記号は $S$ を使います。エントロピーの変化量はエントロピー変化 $\Delta S$（微小なら $\diff S$）で表します。

$$\diff S = \frac{\delta q_\mathrm{rev}}{T} \label{dSdeltaqrev}$$

可逆な熱機関を一周したときのエントロピー変化は次のように表されます。

$$\Delta S = \oint\diff S = \oint\frac{\delta q_\mathrm{rev}}{T} = 0$$

状態量としてのエントロピー

可逆な熱機関を一周したときの変化量が経路にかかわらずにゼロであることから，どうやらエントロピーは新しい状態量のようですが，状態量ならば，系は状態ごとに決まったエントロピーを持っていて，系が別の状態に変化したときは，そこに至った経路にかかわらず変化後の状態のエントロピーは等しくなければなりません。確かめてみましょう。

系がある状態 A から状態 B に可逆な Route 1（$\mathrm{R_1}$）を通って変化し，これとは別のやはり可逆な Route 2（$\mathrm{R_2}$）を通って再び状態 A に戻るとしましょう。

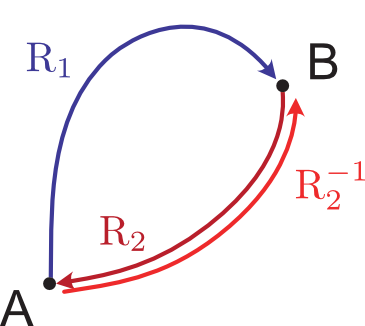
このときのエントロピー変化はゼロになるというのが上の議論の結果です。

$$\Delta S = \oint\diff S = \int_{\mathsf{A},\mathrm{R_1}}^\mathsf{B}\diff S + \int_{\mathsf{B},\mathrm{R_2}}^\mathsf{A}\diff S = 0 \label{r2}$$

次に状態 A から状態 B まで Route 2 を逆行した $\mathrm{R_2^{-1}}$ に沿って進んだとすると，この際のエントロピー変化は（各 $\delta q_\mathrm{rev}$ の符号が逆転するので），Route 2 を進んだ場合とは符合が反転します。

$$\int_{\mathsf{B},\mathrm{R_2}}^\mathsf{A}\diff S = -\int_{\mathsf{A},\mathrm{R_2^{-1}}}^\mathsf{B}\diff S \label{r2inv}$$

式\eqref{r2}と\eqref{r2inv}の結果から次式を得ます。

$$\int_{\mathsf{A},\mathrm{R_1}}^\mathsf{B}\diff S = \int_{\mathsf{A},\mathrm{R_2^{-1}}}^\mathsf{B}\diff S$$

二つのルート $\mathrm{R_1}$ と $\mathrm{R_2^{-1}}$ はどちらも状態 A から状態 B への可逆変化ですが，これらは $\mathrm{R_1}$ と $\mathrm{R_2}$ が任意に定めたルートであるため，互いに異なるルートです。よって，サイクルであるか否かにかかわらず，あるいはそこに至る経路にかかわらず，各状態は（具体的な数値はさておき）決まったエントロピーという状態量を持っており，その変化量は準静的な可逆過程によって状態 A から状態 B に至ったときの式\eqref{dSdeltaqrev}を積分した値に等しくなることが確認できました。すなわち，状態 A と状態 B はそれぞれ状態量としてエントロピー $S_\mathsf{A}$，$S_\mathsf{B}$ を持っていると考えてよく，エントロピー変化は経路にかかわらず $\Delta S = S_\mathsf{B}-S_\mathsf{A}$ となることが分かりました。

不可逆な熱機関のエントロピー変化

次に不可逆な熱機関の場合について考えてみましょう。初めに注意として，エントロピーは状態量ですので経路に依存しません。よって，可逆過程で A から B に行こうが，不可逆過程で A から B に行こうが関係ありません。$\Delta S = S_\mathsf{B}-S_\mathsf{A}$ となります。以下で議論することは，可逆過程であれば $\Delta S$ が $\delta q_\mathrm{rev}/T$ を積分したものと一致したが，これが不可逆であった場合どうなるかということです。

不可逆な熱機関の効率は，熱のやりとりに無駄が生じる，すなわち低温熱源に捨てる分が可逆な熱機関の場合よりも多くなって効率が落ちます。一方，熱源の温度は変わりませんので，式\eqref{reveta}の後半のイコールは成り立ちません。

\begin{align} &\eta_\mathrm{irrev} = 1 - \frac{-q_\mathsf{CD}}{q_\mathsf{AB}} < 1 - \frac{T_\mathrm{L}}{T_\mathrm{H}} \\[3ex] &\Rightarrow\quad -\frac{q_\mathsf{CD}}{q_\mathsf{AB}} > \frac{T_\mathrm{L}}{T_\mathrm{H}} \\[3ex] &\Rightarrow\quad -\frac{q_\mathsf{CD}}{T_\mathrm{L}} > \frac{q_\mathsf{AB}}{T_\mathrm{H}} \quad\Rightarrow\quad \frac{q_\mathsf{AB}}{T_\mathrm{H}} + \frac{q_\mathsf{CD}}{T_\mathrm{L}} < 0 \end{align}

以上の結果と可逆な熱機関の場合の結果をまとめて表記します。

$$\oint\frac{\delta q}{T_\mathrm{ex}} \leq 0 \label{eqclau}$$

式\eqref{eqclau}はクラウジウスの不等式と呼ばれており，等号が成り立つのは可逆な熱機関の場合だけです。不可逆過程の場合（準静的ではないので）系は非平衡な状態を経由します。非平衡状態とは流れだったり勾配だったりがあって系が落ち着いていない状態のことですので，非平衡状態では系の温度は定義できません。そこで，ここでの温度は外界（熱源）の温度であるということを明示するために温度を $T_\mathrm{ex}$ としています。可逆な熱機関の場合はもちろん $T_\mathrm{ex}$ は系の温度 $T$ に一致します。

次は以下のような変化を考えましょう。上との違いは可逆な Route 1（$\mathrm{R_1}$）が不可逆な $\mathrm{R_{irrev}}$ になったことです。

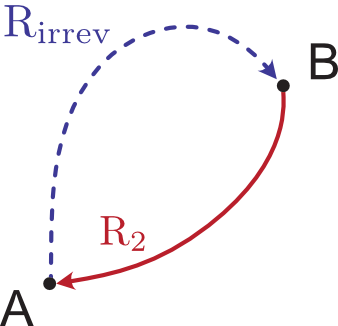
状態 A から状態 B へは不可逆な $\mathrm{R_{irrev}}$ 経由で行き，帰りは可逆な $\mathrm{R_2}$ で戻ります。繰り返しになりますが，エントロピーは状態量なので不可逆過程であっても一周すれば変化量はゼロです。クラウジウスの式\eqref{eqclau}により $\delta q/T$ の積分は以下のようになります。

$$\oint\frac{\delta q}{T_\mathrm{ex}} = \int_{\mathsf{A},\mathrm{R_{irrev}}}^\mathsf{B}\frac{\delta q_\mathrm{irrev}}{T_\mathrm{ex}} + \int_{\mathsf{B},\mathrm{R_2}}^\mathsf{A}\frac{\delta q_\mathrm{rev}}{T} < 0 = \oint\frac{\delta q_\mathrm{rev}}{T} \label{ointirrev}$$

ここで $\Delta S = S_\mathsf{B} - S_\mathsf{A}$ とすると，状態 B から状態 A への変化によるエントロピー変化は $-\Delta S$ ですので，式\eqref{ointirrev}を整理します。

$$\int_{\mathsf{A},\mathrm{R_{irrev}}}^\mathsf{B}\frac{\delta q_\mathrm{irrev}}{T_\mathrm{ex}} + \int_{\mathsf{B},\mathrm{R_2}}^\mathsf{A}\frac{\delta q_\mathrm{rev}}{T} = \int_{\mathsf{A},\mathrm{R_{irrev}}}^\mathsf{B}\frac{\delta q_\mathrm{irrev}}{T_\mathrm{ex}} - \Delta S < 0$$

重要な結論が得られました。まとめます。

系が状態 A から状態 B に変化するとき，変化の途中を細分化して，各変化における熱量の出入り $\delta q$ をそのときの外界の絶対温度 $T_\mathrm{ex}$（ただし変化が可逆過程であるならば，$T_\mathrm{ex}$ は系の絶対温度 $T$ に一致する）で除した $\delta q/T_\mathrm{ex}$ を経路全体に沿って積分すると，この変化における系のエントロピー変化 $\Delta S = S_\mathsf{B} - S_\mathsf{A}$ との間に次式が成立する。

$$\Delta S = S_\mathsf{B} - S_\mathsf{A} \geq \int_\mathsf{A}^\mathsf{B}\frac{\delta q}{T_\mathrm{ex}} \label{me}$$

ただし，等号が成立するのは変化が準静的な可逆過程で行われた場合のみである。

式\eqref{me}を断熱系に適用すると，$\delta q = 0$ ですから積分はゼロになります。

断熱系における変化では，可逆変化ではエントロピーは保存され，不可逆変化ではエントロピーは増大する。

$$\Delta S \geq 0$$

例えば，ある断熱系が定積の部分系 A と定積の部分系 B （つまり外界から仕事はない）に分かれ，両者が取り外しできる壁（あるいはコックのようなもの）で隔てられているとします。部分系 A には気体が入っており，部分系 B は真空としましょう。このとき壁を外す（あるいはコックを開ける）ことで，部分系 A から部分系 B に気体が流れ込み（この過程は非平衡状態を経ます），最終的に両方の部分系に気体が入って巨視的に変化しなくなる熱平衡状態となります。（仕事も熱も出入りしないので）この変化による内部エネルギーの変化はありませんが，不可逆変化ですので，このときの断熱系全体のエントロピーは増大します。

準静的な操作による可逆過程は理想的なもので，現実には系の変化は不可逆に起こりますので，一般に断熱系の内部のエントロピーは系の変化に伴って増大します。これをエントロピー増大の法則と言います。「変化に伴って」ということは，変化しなくなればエントロピーも増大しないわけです。また反対にエントロピーだけ増大して系が変化しないということも（エントロピーは状態量なので）あり得ません。よって，外からの操作が許されない孤立系では，（その条件の下で）系のエントロピーが最大値をとることと，系が熱平衡状態であることは同値となります。先ほどの定積の部分系 A と定積の部分系 B に分かれた断熱系で，A と B にはそれぞれ酸素と窒素が入っていて互いに熱平衡状態にあるとしましょう。壁を外すと酸素と窒素は混合し始めます。途中は非平衡状態なのでエントロピーを定義できませんが，最終的に熱平衡状態に達したとき（すなわち均一に気体が混ざり合ったとき）のエントロピーは，この条件の下でとることが許されるエントロピーの最大値となります。

断熱系ではない場合は，エントロピー増大の法則は成り立たず，エントロピーが減少しても構いません。冷凍庫に水を入れたら氷になってエントロピーが減少したというのは，系（水）は断熱系ではない（冷凍庫との間で熱量の移動がある）のでエントロピー増大の法則と矛盾しません。「いつ何時もエントロピーは増大するものだ」と勘違いする人がいますので注意が必要です。ただし，水も冷凍庫もその置かれている部屋も地球も宇宙もすべてを一つの系とみなした場合，これは（壮大な）断熱系と見ることもできますので，一般に私たちが外界と考える部分もすべて込みの宇宙全体のエントロピーは常に増大します。

さて，式\eqref{me}の不等号の出処を遡って考えてみると，それはトムソンの原理（一つの熱源から熱を受け取り，他に何の影響も残さず，これをすべて仕事に変えて元の状態に戻るサイクルはできない）です。トムソンの原理を受け入れたから，熱機関の原理的な最大効率が決まり，エントロピーという状態量が導入され，可逆な熱機関の熱比で定義された熱力学的温度（絶対温度）と熱比との大小関係が決まり，式\eqref{me}の導出に至ったわけです。

トムソンの原理は熱力学第二法則の表現の一つですから，結果としてエントロピー $S$ は式\eqref{me}を通じて第二法則を表しており，$U$ とともに系を特徴づける状態量であることが分かります。この意味で，体積，圧力，温度，物質量（粒子数），エンタルピーなど系が熱平衡状態であれば一意に定まる状態量には色々な種類がありますが，内部エネルギー $U$ とエントロピー $S$ は系を特徴づけるための状態量として特別な存在です。