エントロピーの性質

前節までの議論でエントロピー $S$ が状態量であることが分かりました。ではエントロピーは具体的にどのくらい変化するのか。あるいはエントロピーの具体的な値を求めることはできるのか。エントロピーの性質について考察します。

理想気体の等温膨張過程におけるエントロピー変化

理想気体の温度を一定値 $T$ に保ち，状態 A から状態 B に準静的に膨張させたときのエントロピー変化を求めてみましょう。これは既に議論した，理想気体を作業物質としたカルノーサイクルの AB 過程に相当しますので，既に $\delta q$ は求まっています。

\begin{align} &\delta q_\mathrm{rev} = \frac{nRT}{V}\diff V\\[3ex] &\Delta S_\mathsf{AB} = nR\int_\mathsf{A}^\mathsf{B}\frac{\diff V}{V} = nR\ln\frac{V_\mathsf{B}}{V_\mathsf{A}} = nR\ln\frac{P_\mathsf{A}}{P_\mathsf{B}} > 0 \end{align}

これより，準静的な等温膨張過程により系のエントロピーは増加することがわかります。しかもその変化量は物質量 $n$ に比例しますので，エントロピーは示量性状態量であることが確認できます。反対に，等温圧縮過程であれば系のエントロピーは減少します。

外界から系に $\delta q_\mathrm{rev}$ の熱量が入るとき，外界にとっての熱量の出入りは $-\delta q_\mathrm{rev}$ ですので，外界のエントロピー変化 $\Delta S_\mathrm{ex}$ は $\Delta S_\mathrm{ex} = -\Delta S_\mathsf{AB} < 0$ となります。すなわち（可逆過程なので）系で増加した分のエントロピー変化は外界で減少した分のエントロピー変化と相殺し，系と外界を合わせた全体のエントロピーは変化しません。これが（前節で触れた）可逆変化であれば宇宙全体のエントロピーは変化しないということの意味です。

定圧で系の温度を変化させたときのエントロピー変化

エントロピーは状態量なので，状態に至った経路に依存せず，その意味では熱量 $q$ よりも扱いやすい存在です。しかし，だからと言って，今後は $q$ は使わずにエントロピー $S$ だけを使えばよいかというと，そうもいきません。熱量 $q$ にはエントロピーが持っていない「実験的に測定するのが容易」という重要な特徴があります。系にどのくらいの熱量を与えるかは，例えば電熱線に流す電流によりコントロールできますので実験的に決定が可能です。一方，エントロピーがいくら状態量だからと言って，系のエントロピーを直接測る測定器があるかというと，そのようなものはありません。あくまでも準静的とみなせるような条件で熱の出入りを測る必要があります。

定圧条件で系に外界から熱を準静的に（とみなせるようにゆっくりと）加えたとき，加えた熱量 $\delta q_{p,\mathrm{rev}}$ はエンタルピーの微小変化 $\diff H$ に一致します（本編 > エンタルピー）。ここで，定圧熱容量 $C_p$ の定義（本編 > 熱容量）を思い出すと，次式が成立しています。

$$\delta q_{p,\mathrm{rev}} = \diff H = C_p\,\diff T \label{dqdh}$$

式\eqref{dqdh}を使えば，系に熱量 $\delta q_{p,\mathrm{rev}}$ を加えたときの系のエントロピー変化 $\diff S$ が次式で求まります。

$$\diff S = \frac{\delta q_{p,\mathrm{rev}}}{T} = \frac{C_p}{T}\diff T$$

温度が $T_1$ から $T_2$ に変化したときのエントロピー変化 $\Delta S$ はこの式を積分すれば求まります。

$$\Delta S = \int_{T_1}^{T_2}\frac{C_p}{T}\diff T \label{DSCp}$$

もし注目している温度領域の $C_p$ が分かっていて，しかも（温度範囲が狭いなどの理由で）$C_p$ が一定とみなせるのであれば，式\eqref{DSCp}の計算は簡単です。

$$\Delta S = C_p\int_{T_1}^{T_2}\frac{\diff T}{T} = C_p\ln\frac{T_2}{T_1}$$

しかし，実際には本編 > 熱容量の実際で見たように，$C_p$ は温度により変わりますので，安易に積分の外に $C_p$ を出すことはできません。その場合は，$C_p$ の温度依存性を実験で決定するか，あるいは既に示したようにデータベースに代表的な温度の $C_p$ が報告されているのであれば，実験値にフィットするような関数を用意してから積分を行う必要があります。

また，一次相転移が起こる温度領域を含む場合は注意が必要です。下図の上段は水の温度と定圧熱容量 $C_p$ の関係を示したグラフですが，融点と沸点では $C_p$ が発散していることが分かります。一次相転移点では系に熱を与えても（$\Delta H > 0$）温度変化がない（$\diff T = 0$）わけですから，定義を考えれば $C_p$ が無限大に発散するのは当然です。

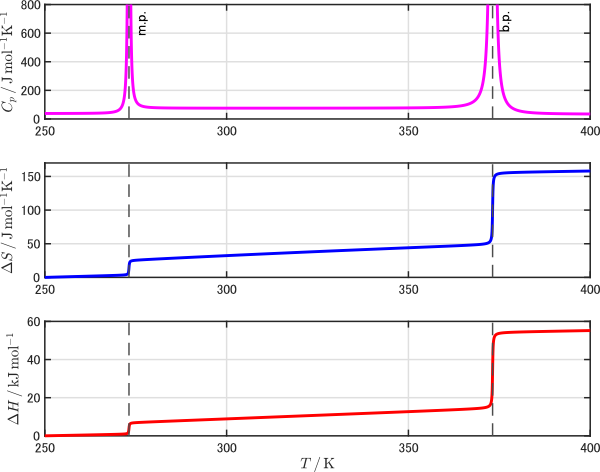
水の相転移に伴う $C_p$，$\Delta H$，$\Delta S$ の変化

このような場合は，相転移部分で分割し，相転移に伴う熱の移動はエンタルピー変化で計算するのが定法です。融点以下の温度 $T_\mathrm{i}$ から沸点以上の温度 $T_\mathrm{f}$ の範囲でのエントロピー変化を求めるのであれば次のようになります。

$$\Delta S_\mathrm{m} = \int_{T_\mathrm{i}}^{T_\mathrm{fus}^<}\frac{C_{p,\mathrm{m}}^\mathrm{solid}}{T}\diff T + \frac{\Delta_\mathrm{fus}H_\mathrm{m}}{T_\mathrm{fus}} + \int_{T_\mathrm{fus}^>}^{T_\mathrm{vap}^<}\frac{C_{p,\mathrm{m}}^\mathrm{liquid}}{T}\diff T + \frac{\Delta_\mathrm{vap}H_\mathrm{m}}{T_\mathrm{vap}} + \int_{T_\mathrm{vap}^>}^{T_\mathrm{f}}\frac{C_{p,\mathrm{m}}^\mathrm{gas}}{T}\diff T$$

$T_\mathrm{fus}^<$ は融点未満（ぎりぎり手前）の温度までという意味です。fus は融解（fusion），vap は蒸発（vaporization）の略で，例えば $\Delta_\mathrm{vap}H_\mathrm{m}$ はモル蒸発エンタルピーとなります。他の記号についても誤解はないかと思います。

熱力学第三法則

エントロピーの変化量は定圧熱容量の温度依存性や相転移の際のエンタルピー変化から求めることができますが，ある状態でのエントロピーの具体的な数値というのは変化量だけからは求まりません。何か基準があれば，その基準からの変化量を求めることで，具体的なエントロピーの値を求めることができます。

様々な純物質の熱容量の温度依存性が調べられた結果，固体状態では温度を下げるほどエントロピーの変化が小さくなり，ある下限値に漸近していくように見えるという観測結果が得られました。つまりエントロピーにはある下限があって，低温になるほどその下限に漸近していくのではないかということが実験により示唆されました。世の中のすべての物質について調べられたわけではないですが，この傾向は普遍的であると考えられ，それを公理として受け入れ，その下限をエントロピーの基準値 $S=0$ と定めたのが熱力学第三法則です。

すべての純物質の完全結晶のエントロピーは $0\unit{K}$ で $S=0$ となる。
すべての純物質の完全結晶に対し，任意の準静的な可逆変化におけるエントロピー変化 $\Delta S$ は，圧力に依らず $T \to 0$ の極限でゼロに近づく。

一番目の方がやや簡易な表現になります。混合物の場合は，混合による分のエントロピーがありますので，$0\unit{K}$ だからといってエントロピーが下限に達しませんので純物質に限定しています。完全結晶というのは欠陥のない完ぺきに原子の並びが揃った結晶という意味ですが，当然，理想化されたもので，実際に存在するものではありません。

この基準を受け入れるならば，純物質のある状態におけるエントロピーの具体的な値が原理的に求まります。求めたい状態の温度からできるだけ低温までの熱容量の温度依存性を実験的に求め，あるいは低温領域では理論モデルによる予測値も活用し，最終的には $0\unit{K}$ での熱容量に外挿してあげれば，その結果を使って，その状態のエントロピーの具体的な値を決定することができます。これはあくまでも第三法則の基準を受け入れたことで求まった値ですので，このようにして決定したエントロピーを第三法則エントロピーと呼びます。

完全結晶ではない純物質の場合，$T=0$ でも $S=0$ にはなりません。実験的に $T=0$ に近づけても $S > 0$ である場合，これを残留エントロピーといいます。この場合は，$T = 0$ における残留エントロピー $S_0$ を既知の基準値として取り扱い，そこからのエントロピー変化を積分により求めることで，目的の温度におけるエントロピーの値が計算できます。