理想気体の断熱変化

閉じた系のピストン付き容器に入った理想気体を温度 $T_\mathrm{i}$，体積 $V_\mathrm{i}$，圧力 $p_\mathrm{i}$ の始状態 $(T_\mathrm{i},V_\mathrm{i},p_\mathrm{i}$) から，終状態 $(T_\mathrm{f},V_\mathrm{f},p_\mathrm{f})$ に変化させたときの内部エネルギー変化 $\Delta U$ を考えましょう。三つの変数がありますが独立なのはこのうちのいずれか二つで，三つのうち二つが決まれば残った一つは状態方程式により自動的に決まります。内部エネルギーは状態量で経路には依存しませんので，理解しやすくするために，実際の変化を二段階に分けた仮想的な考察を行いましょう。まずは体積だけを変化させ，後半に温度を変化させる（その結果圧力は自動的に $p_\mathrm{f}$ になる）という二段構えで考えます。

はじめに系の温度を $T_\mathrm{i}$ に保ったまま（等温条件），外圧を操作してピストンを動かして仕事を与えるなどして，体積を $V_\mathrm{i}$ から $V_\mathrm{f}$ に変化させます。その結果，圧力はもはや $p_\mathrm{i}$ ではなくなりますが，閉じた系では理想気体の内部エネルギーは温度のみの関数 $U=U(T)$ で体積や圧力には依存しません。このため，温度を一定に保ったまま体積を変化させても内部エネルギーは変化しません。次に（ピストンを固定して）体積を $V_\mathrm{f}$ に保ったまま（定積条件），温度が $T_\mathrm{i}$ から $T_\mathrm{f}$ になるまで，系に熱量 $q$ を与えます。この過程での圧力は自動的に $p_\mathrm{f}$ になります。定積熱容量 $C_V$ の値は理想気体のタイプによりますが，温度依存性はありません。よって，この後半の過程での内部エネルギー変化は次のように書けます。

$$\Delta U = q = (T_\mathrm{f}-T_\mathrm{i})C_V = C_V\Delta T$$

今は後半の温度変化を熱により実現しましたが，内部エネルギーは状態量なので，終状態が同じであれば，エネルギーを熱で与えようと仕事で与えようと結果としての $\Delta U$ は同じであり，もし，$C_V\Delta T$ に相当するエネルギー変化を熱ではなく仕事 $w$ で系に与えたとしても，上の二段構えのプロセスの終状態と同じ状態が得られるはずです。そこで，次は $(T_\mathrm{i},V_\mathrm{i},p_\mathrm{i}$) から $(T_\mathrm{f},V_\mathrm{f},p_\mathrm{f})$ への変化を断熱条件（adiabatic condition）で行うことを考えます。断熱条件とは，外部からの熱の出入りがない状況を指します。この場合，系に出入りするエネルギーは仕事だけになるので，先ほど熱で与えたエネルギーを仕事 $w$ で与えれば，すなわち $w = C_V\Delta T$ を与えれば同じ終状態が得られるはずです。

この断熱過程において，仕事を準静的に与えたとしましょう。理想気体の状態方程式を考慮して以下が成り立ちます。

\begin{align} &\delta w = C_V\diff T = -p\,\diff V \\[3ex] &\Rightarrow C_V\diff T = -\frac{nRT}{V}\diff V \\[3ex] &\Rightarrow C_V\int_{T_\mathrm{i}}^{T_\mathrm{f}}\frac{\diff T}{T} = -nR\int_{V_\mathrm{i}}^{V_\mathrm{f}}\frac{\diff V}{V} \\[3ex] &\Rightarrow C_V\ln\frac{T_\mathrm{f}}{T_\mathrm{i}} = nR\ln\frac{V_\mathrm{i}}{V_\mathrm{f}} \\[3ex] \end{align}

ここで式を簡潔にするために無次元量 $c$ を $c \equiv C_V/nR = \Cvm/R$ で定義すると次式になります。

\begin{align} &\left(\frac{T_\mathrm{f}}{T_\mathrm{i}}\right)^c = \frac{V_\mathrm{i}}{V_\mathrm{f}} \label{vif}\\[3ex] &\Rightarrow V_\mathrm{i}T_\mathrm{i}^c = V_\mathrm{f}T_\mathrm{f}^c \label{poi} \end{align}

すなわち理想気体の準静的断熱過程においては，常に $VT^c$ が一定に保たれるという結果になりました。

実際のプロセスをイメージすると，外圧を少しずつ変えて，その結果としてピストンが動いて体積が変化すると考える場合も多いでしょうから，$V$ と $T$ の関係に加え $p$ と $V$ の関係も知っておきたいです。状態方程式と式\eqref{vif}より次式が成り立ちます。

\begin{align} &\frac{p_\mathrm{i}V_\mathrm{i}}{p_\mathrm{f}V_\mathrm{f}} = \frac{T_\mathrm{i}}{T_\mathrm{f}} = \left(\frac{V_\mathrm{f}}{V_\mathrm{i}}\right)^{1/c} = \left(\frac{V_\mathrm{i}}{V_\mathrm{f}}\right)^{-1/c}\\[3ex] &\Rightarrow \frac{p_\mathrm{i}}{p_\mathrm{f}}\left(\frac{V_\mathrm{i}}{V_\mathrm{f}}\right)^{1/c + 1} = 1 \end{align}

理想気体で成り立つマイヤーの関係式 $\Cpm - \Cvm = R$ を利用して $\gamma$ を定義します。

$$\gamma \equiv \frac{1}{c}+1 = \frac{1+c}{c} = \frac{R + \Cvm}{\Cvm} = \frac{\Cpm}{\Cvm}$$

よって $p$ と $V$ には次の関係が成り立ち，理想気体の準静的断熱過程においては，常に $pV^\gamma$ が一定に保たれることになります。

$$p_\mathrm{i}V_\mathrm{i}^\gamma = p_\mathrm{f}V_\mathrm{f}^\gamma$$

理想気体の状態方程式（あるいはボイルの法則）は，準静的過程において等温条件（断熱ではなく熱の出入りが許される）であれば $pV$ が一定に保たれるというものでした。一方で，断熱条件であれば系の温度は変化しますが，その場合でも $pV^\gamma$ は一定に保たれます。すなわち，断熱条件下では温度が変化するものの，$pV^\gamma$ が一定に保たれることで，熱の出入りなしに，内部エネルギーの変化が外部への仕事とつり合い，エネルギー保存（第一法則）が成り立つと理解できます。

理想気体のタイプ別 $c$ と $\gamma$ の値
タイプ	$\Cvm\,/\JKmol$	$\Cpm\,/\JKmol$	$c$	$\gamma$
単原子分子	$\frac{3}{2}R$	$\frac{5}{2}R$	$\frac{3}{2} = 1.5$	$\frac{5}{3} \approx 1.67$
線形分子	$\frac{5}{2}R$	$\frac{7}{2}R$	$\frac{5}{2} = 2.5$	$\frac{7}{5} = 1.40$
非線形分子	$3R$	$4R$	$3$	$\frac{4}{3} \approx 1.31$

下のグラフは $1\unit{mol}$ の単原子分子理想気体を様々な温度での等温過程（青線）あるいは初期値の圧力と体積をいろいろに変えた断熱過程（赤線）で変化させたときの $p\,\text{-}V$ 曲線を多数重ねてプロットしたものです。青線と赤線で囲まれた（菱形のような）領域が多数つくられているのが分かります。曲線の形状は気体の種類によって多少変わりますが，後で学ぶ本編 > カルノーサイクルでは，この菱形面積分の仕事を準静的に取り出すことで，熱から取り出すことができる仕事の最大値を求めることになります。

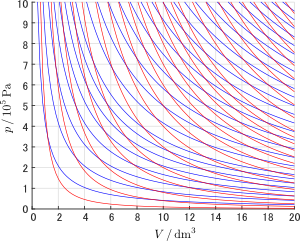
単原子分子理想気体をさまざまな条件の初期状態から等温過程（青色）または断熱過程（赤色）で操作したときの体積と圧力の関係