気体の状態変化

前節で登場したピストン付き密閉容器に入った気体に対して，熱や仕事をあれやこれやしてあげることで，色々な気体の状態をつくることができます。自由にあれやこれやしても構いませんが，特徴が出やすいような変化の方が議論には何かと便利です。主に以下に述べるような気体の状態変化を考えることが多いです。

定積変化

定積変化は，気体の体積が一定で変化しない状態の変化です。等積変化ともいいます。具体的にはピストンをがっちり固定して動かなくしてしまえば定積になります（そもそも，ピストンである必要はないですが）。ピストンが動かないと，気体に対して仕事をすることはできませんし，気体が仕事をすることもできません。一方，熱の出入りは制限していませんので，内部エネルギーの変化は気体に与えられた熱量だけに依存します。

熱量 $q > 0$ を気体に与えると，気体の温度 $T$ が上昇しますので，理想気体の状態方程式より，気体の圧力 $P$ も上昇します。

定圧変化

定圧変化（等圧変化）は，体積は変化して良い一方，気体の圧力が一定に保たれる変化です。ピストンが自由に動き，容器の外側の圧力（外圧）が一定であれば，内部の気体の圧力 $P$ は，常に外圧と等しく，一定になります。定積変化と違ってピストンが動くので，気体に対する仕事を考えなくてはいけません。ピストンの面積を $S$ とすると，ピストンの面全体にはたらく力は $PS$ です。この力でピストンが $L$ 動いたとすると，仕事は $PSL$ で表されますが，$SL$ は気体の体積変化に他なりませんので，これを $\Delta V$ と書くことにすると，気体がなす仕事 $\overline{w}$ は $P\Delta V$ となります。$w$ は気体になされる仕事ですから，符号を反転させます。気体の体積が減少するときが正のなされる仕事になりますので，マイナス記号がつくことに注意してください。速習編で触れたように，エンタルピーの学習で活躍する変化です。

等温変化

前節で単原子理想気体分子の内部エネルギーが絶対温度に比例することを学んだように，温度と内部エネルギーとは直接的な関係があります。温度を一定に保つ等温変化というのは，$q$ と $\overline{w}$ のバランスがとれていて，差し引きゼロの変化です。つまり，熱量 $q$ を加えたら，$q$ と同じだけの仕事を気体がなすということです。気体が膨張するんだから定圧変化と同じじゃないの？と思うかもしれませんが，等温変化は温度が変化しないようにピストンを外から押す力を絶妙にコントロールしながら熱量 $q$ を与える，職人技が求められる変化です。

断熱変化

これまでは熱の出入りが先にあって，それに合わせてピストンをどうするか（固定する，自由に動く，温度が一定になるように調節する）という順番でした。断熱変化は，文字通り熱の出入りを断つ変化です。ですので，ピストンを押すか引くかしない限り，何も変化しません。内部エネルギーの変化は仕事のみに依存します。断熱された気体に仕事をすれば（圧縮すれば），内部エネルギーが増加するので，温度が上がります。

気体になされる仕事

定圧変化において，気体になされる仕事が $-P\Delta V$ であることを上で学びました。等温変化や断熱変化でも，圧力と体積変化の積で仕事を求めることができますが，定圧変化と違って，体積の変化に伴い，圧力も変化しますので，$-P\Delta V$ では具合が悪いです。$V$ を微小量ずつ変化させていき，それぞれの場合の $P$ をかけたものを積分すれば，圧力が体積に依存する場合でも，気体になされる仕事を表すことができます。

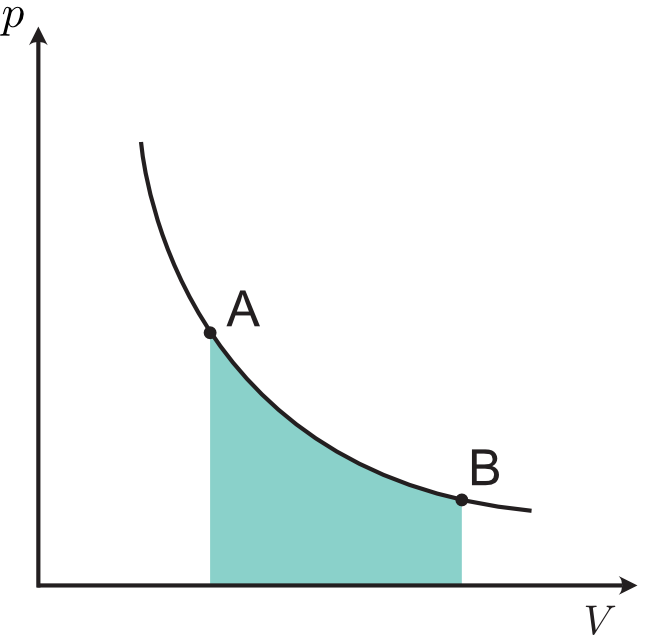
気体の体積を横軸，圧力を縦軸にとって，状態変化に伴う体積と圧力の変化をグラフに表すことができ，これを $P$-$V$ 図といいます。下に示す $P$-$V$ 図で，気体の状態が A 点からグラフに沿って B 点まで変化したとき，気体が「なした」仕事は，式(\ref{workPdV})から分かるように，図で色付けした部分の面積に一致します。定圧変化の場合，色付け部分が長方形となるため，$P\Delta V$ で面積を求めることができるわけです。