内部エネルギーの全微分

熱力学で扱う状態関数は数学的には多変数関数ですので，講義 > 補足 > 偏微分と全微分で説明した全微分の取り扱いをすることができます。全微分可能であるためには $C^1$ 級（偏微分可能ですべての偏導関数が連続）という条件がありますが，まずは条件を気にせず，状態関数を形式的に全微分の形にしてみます。

第一法則より，気体の体積変化のみを仕事とする準静的過程では以下が成り立つことを前節で示しました。

式\eqref{tspv}の形を（物理的な意味はとりあえず考えずに）形式的に見てみると，全微分の形で書かれていることが分かります。全微分とは，多変数関数において複数の変数が同時に変化したとき，各変数方向の変化率（偏微分係数）と微小変化量の積の和が全体の微小変化量になるということです。すなわち，状態関数 $U$ は，変数を $S$ と $V$ とする多変数関数 $U = U(S,V)$ であり，$U$ の $S$ 軸方向の変化率（偏微分係数）である $\left(\dfrac{\partial U}{\partial S}\right)_V$ が $T$ であり，$U$ の $V$ 軸方向の変化率である $\left(\dfrac{\partial U}{\partial V}\right)_S$ が $-p$ に対応していることになります。

式\eqref{defT}の意味するところは次の 2 点です。

一番目の「エントロピーを変化させたときの内部エネルギーの変化率」は何ともイメージのしにくい量ですが，状態関数を数学的に処理することで温度がこのように表される点は重要です。この形式を重要視し，むしろこれを熱力学的温度の定義として議論を展開する説明の仕方もあります。$U$ も $S$ も示量性状態量であり，示量性状態量どうしの変化率が示強性状態量である $T$ になっている点に注意してください。圧力 $p$ についても同様で，示量性状態量どうしの変化率になっています。このように，状態関数の変数として示量性状態量を選んでおいて，これを全微分の形で書くと，その偏微分は示強性状態量になります。

二番目の「$T$ が従属関数」というのは，状態関数の変数として何を選ぶかという点から重要です。$S$ と $V$ は $U$ に対して独立した変数であるのが特徴で，このような変数の組を自然な変数（natural variables）と呼んでいます。すなわち，自然な変数とは，ある状態関数を全微分したときに現れる独立変数の組を指します。$T$ は $U$ の偏微分で表されますが，$U$ をどう偏微分しても $S$ も $V$ も出てこないというのが従属変数と独立変数の違いです。圧力 $p$ は $T$ と同様に従属変数ですので自然な変数ではありません。

状態関数を自然な変数で表すことで，全微分の形において，その偏微分係数が温度や圧力などの物理的意味を持つ示強性状態量として現れ，状態関数に関する情報を明示的かつ最大限に表現することができます。例えば，$U$ の変数として自然な変数ではない温度 $T$ と圧力 $p$ を選び $U = U(T, p)$ としたらどうなるでしょうか。エントロピー $S$ は測定しにくいですし，大気圧下であれば圧力 $p$ は一定になるのでこちらの表記の方が便利そうです。形式的に全微分してみます。

式\eqref{utp}中の$\left(\dfrac{\partial U}{\partial p}\right)_T$ は，温度一定で圧力を変えたときの内部エネルギーの変化率という意味ですが，これには体積変化が伴うので，結局，分子間の距離が離れる（近づく）ことによって内部エネルギーがどう変わるかということを表していることになり，分子間の相互作用に起因する項ということになります。理想気体であれば分子間の相互作用がないので，この偏微分係数はゼロになり（分子間の距離が変わっても内部エネルギーに影響がない），式\eqref{utp}の右辺第二項がゼロになるので，内部エネルギーが温度 $T$ だけの関数になることが分かります。そういえばこの偏微分，本編 > 熱容量のジュールの法則で出てきたな，と気付いた方は鋭い観察眼をお持ちです。

さて $U=U(S,V)$ と $U=U(T,p)$ は，どちらも内部エネルギー $U$ を表す関数として等価なものでしょうか。実は違います。前者の $U=U(S,V)$ は（外界との物質のやり取りができない閉じた系であれば）$S$ と $V$ を定めれば，系の巨視的な状態が一つに定まります。逆も真で，系の状態が定まれば $S$ と $V$ は一つに定まり，結果として $U$ も定まります。すなわち，状態関数 $U(S,V)$ の値域と系の各状態の間には全単射（1 対 1 対応）の関係があり，$S$ と $V$ により系の熱力学的な状態のすべてを定めることができます。「温度は？圧力は？」と思うかもしれませんが，これらの状態量は式\eqref{defT}，式\eqref{defp}により $U$ と従属の関係がありますので，温度 $T$ と圧力 $p$ は $S$ と $V$ から一意に定まります。一方，後者の $U=U(T,p)$ はそうはいきません。系が熱平衡状態にあれば，$T$ と $p$ は定まりますが，逆に $T$ と $p$ が定まったからと言って，状態が一つに定まるとは限りません。例えば，定圧条件で液体の水と気体の水（水蒸気）が気液平衡の状態にあるとします。$1\unit{atm}$ であれば $100\oC$ で気液平衡になります。このとき，系にさらに熱を加えると内部エネルギーは変化し，それに伴い，液体の水と水蒸気の割合は変化しますが，液体の水が残っている限りは（熱平衡状態での）系の温度は変化しません。液体と気体の比率が異なる状態は互いに異なる状態で，気体の割合が増えるほど内部エネルギーもエントロピーも増加しています。しかし，液体の水が完全になくなるまでは，系に熱を与えても，温度（定圧なのでもちろん圧力も）は変化しません。よって，温度 $T$ と圧力 $p$ を与えただけでは系の状態を一意に定めることができない（場合がある）ことが分かります。

両方の状態変数を変えたのはやりすぎたかな？ということで，$U=U(T,p)$ のうち，$p$ のみを $V$ に戻して $U=U(T,V)$ として，全微分を考えてみます。

$\left(\dfrac{\partial U}{\partial T}\right)_V$ は見覚えがありますね。体積一定で温度に対する内部エネルギーの変化率，これは定積熱容量 $C_V$ です。$\left(\dfrac{\partial U}{\partial V}\right)_T$ の方は内部圧 $\pi_T$ と呼ばれているのですが，その意味するところは，温度一定で，体積を変えたときに内部エネルギーがどう変化するかということです。これは分子間の相互作用に起因するものであり，理想気体であれば分子間の相互作用がないので，内部圧もゼロになり（分子間の距離が変わっても内部エネルギーに影響がない），式\eqref{utv}の右辺第二項がゼロになるので，内部エネルギーが温度 $T$ だけの関数になることが分かります。やはりこの偏微分，本編 > 熱容量のジュールの法則で出てきましたね。

さて $U=U(T,V)$ の値域は状態と全単射の関係にあるでしょうか。残念ながら，この場合も定積条件で水の気液平衡を考えたとき，同じ温度で気液の割合が異なる状態が存在しますので，温度 $T$ と体積 $V$ を与えただけでは系の状態を一意に定めることができない（場合がある）ことになります。

もちろん，$U=U(S,V)$ 以外の表示でも沸点や凝固点でなければ状態が一意に定まりますし，$T$ は測定しやすいというメリットもありますので，目的に応じて適切な状態関数を使うというのが結論ですが，系のすべてを表すことができるわけではないという事実は重要です。

さらに言うと，$T$ が同じでも $U$ が変化する領域があるわけで，横軸を $T$，縦軸 $U$ としてグラフを描いたときに，下図のように $U$ の値がある $T$ でジャンプすることになります。そうすると，そもそもその温度では関数が $C^1$ 級の条件を満たしませんので，その温度を跨いで全微分をとること自体が数学的にできないということになります。

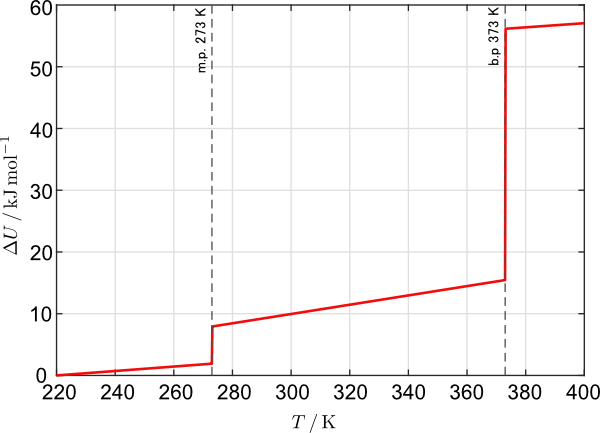
定圧条件における水の相転移を含む内部エネルギー変化

状態関数と状態変数は入れ替えが可能ですから，$S=S(U,V)$ として全微分した式\eqref{dsuv}と，式\eqref{tspv}を変形した式\eqref{stupt}を比べてみます。

式\eqref{suvt}と式\eqref{iTpT}の関係は式\eqref{defT}と式\eqref{defp}から導かれますので，$U=U(S,V)$ と $S=S(U,V)$ は関数としては等価になります。$U$ と $V$ は $S$ の自然な変数で，$S=S(U,V)$ も系の熱力学的状態を余すところなく表すことができる関数です。