ラチマー図

化学種の標準電極電位は表を見れば分かりますが，ある物質が何段階かの酸化還元反応を示すとき，各段階が一目で分かるようにまとまっていると便利で，これをラチマー図（Latimer diagram）といいます。ラチマー図では着目する元素について，酸化数の最も高い状態を一番左に書き，そこから還元されて酸化数が小さくなる順に化学種を書き，それらを結ぶ矢印の上に標準電極電位を書きます。$\ce{H+}$ や $\ce{H2O}$ などは省略する約束です。実例を見てみましょう。

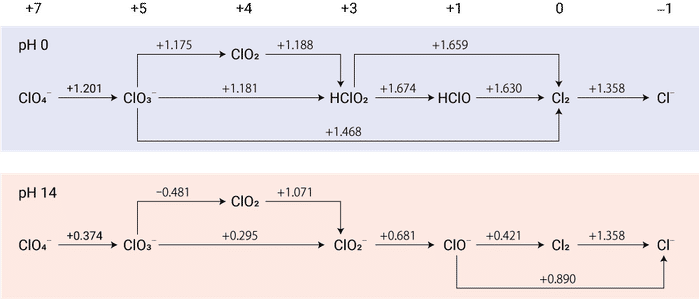
塩素のラチマー図

このラチマー図は塩素に関するもので，酸化数が一番大きい $+7$ の過塩素酸イオン $\ce{ClO4-}$ が一番左に書いてあります。上は酸性条件 $\pH\,0$，下は塩基性条件 $\pH\,14$ でのラチマー図です。例えば $\ce{ClO4- ->[+1.201] ClO3-}$ や $\ce{ClO3- ->[+1.175] ClO2}$ および $\ce{HClO ->[+1.630] Cl2}$ とあるのは，それぞれ以下のように解釈します。

\begin{alignat}{3} &\ce{ClO4-(aq) + 2H+(aq) + 2e- -> ClO3-(aq) + H2O(l)} &\hspace{2cm} &\Eo = +1.201 \unit{V} \label{Latione} \\[7pt] &\ce{ClO3-(aq) + 2H+(aq) + e- -> ClO2(aq) + H2O(l)} &\hspace{2cm} &\Eo = +1.175 \unit{V} \label{Latitwo} \\[7pt] &\ce{HClO(aq) + H+(aq) + e- -> 1/2Cl2(g) + H2O(l)} &\hspace{2cm} &\Eo = +1.630 \unit{V} \label{Latithree} \end{alignat}

いずれも左辺にプロトンを含むため，電極電位は $\pH$ に依存します。$\pH\,14$ のとき，反応（\ref{Latione}）ではプロトン数と電子数がどちらも $2$ なので $E=+1.201 - 0.0591\times14 = +0.374 \unit{V}$ となります。一方（\ref{Latitwo}）では関わるプロトン数が $2$，電子数が $1$ なので $E=+1.175 - 2\times 0.0591\times14 = -0.480\unit{V}$となり，上の酸性条件のラチマー図と下の塩基性条件のラチマー図が対応します。なお $\Eo(\ce{Cl2},\ce{Cl-})$ は反応にプロトンが関わらず $\pH$ の影響を受けないのでどちらの図でも $\ce{Cl2 ->[+1.358] Cl-}$ と同じ数字が書いてあります。

ラチマー図の隣り合っていない電極電位を求めるには，各々の電極電位の和を求めるのではなく，$\DGo{r}=-\nue F\Eo$ を用いて各ステップのギブズエネルギー変化の和を求め，それを電極電位に変換する必要があります。実はこれは $\Eo(\ce{Fe^{3+}},\ce{Fe})$ を求める演習として既に解説をしています。例えば酸性条件での $\ce{ClO4-}$ から $\ce{HClO2}$ の 2 段階をまとめたときの標準電極電位を求めてみましょう。関わる電子数に注意が必要ですが，図の一番上に酸化数が書いてありますので酸化数の減少分が電子数になります。

\begin{align} &\DGo{r}(\ce{ClO4- -> HClO2}) = \DGo{r}(\ce{ClO4- -> ClO3-}) + \DGo{r}(\ce{ClO3- -> HClO2})\\[7pt] &-4F\Eo(\ce{ClO4- -> HClO2}) = -2F\Eo(\ce{ClO4- -> ClO3-}) -2F\Eo(\ce{ClO3- -> HClO2}) \end{align}

これより $\ce{ClO4- -> HClO4}$ の標準電極電位は次式で求まります。

$$\Eo(\ce{ClO4- -> HClO2}) = \frac{2\Eo(\ce{ClO4- -> ClO3-}) + 2\Eo(\ce{ClO3- -> HClO2})}{4} = 1.191 \unit{V}$$

同様の考え方を用いると $\ce{ClO3- -> Cl2}$ の標準電極電位は以下のように求まります。この結果は既に図に書いてあります。どこからどこへのジャンプが図に描かれるかは決まっておらず，よく使う（と作図者が考えた）ものが描かれていますので，参考にする図によって違った描き方になっていることもありますが，必要であれば自分で求めることができます。

$$\frac{2\times 1.181 + 2\times 1.674 + 1.630}{5} = +1.468 \unit{V}$$

ラチマー図において，ある化学種を中心に見て，より酸化数が大きい化学種からその化学種への電極電位よりも，より酸化数が小さい化学種への電極電位の方が大きい，すなわち，左よりも右の電極電位の方が大きいとき，その化学種は不均化します。前節で $\ce{Cu+}$ イオンの不均化を議論しましたのでラチマー図を確認してみましょう。

銅のラチマー図

確かに $\ce{Cu+}$ を中心に見たときの左側よりも右側の電極電位が大きく書かれています。この不均化は $\ce{Cu+}$ イオンが酸化剤と還元剤の両方の役割をすることによって起こります。あえてくどい書き方をするのであれば次のようになります。

$$\ce{Cu+ + Cu+ -> Cu^{2+}} + \ce{Cu}$$

還元剤としてはたらくときは自身は酸化されますので，電極電位としては $\ce{Cu^{2+}}$ の電位を見ます。するとこの反応の $\Eocell$ は次式で書かれます。

$$\Eocell = \Eo(\ce{Cu+},\ce{Cu}) - \Eo(\ce{Cu^{2+}},\ce{Cu+})$$

この不均化反応は $\Eo(\ce{Cu+},\ce{Cu}) > \Eo(\ce{Cu^{2+}},\ce{Cu+})$ のとき，すなわちラチマー図で右側の数字が左側よりも大きいときに $\Eocell > 0$ となって自発的に進むことが分かります。