田辺・菅野ダイヤグラム４

$\ao{d}^8$ 電子配置

$\ao{d}^8$ 電子配置の田辺・菅野ダイヤグラムを示します。

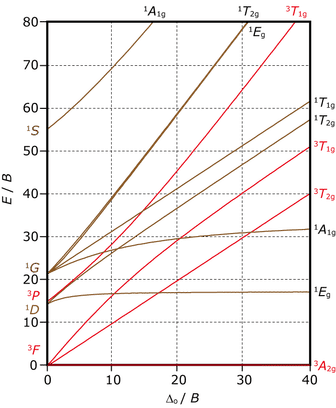
$\ao{d}^8$ 電子配置の田辺・菅野ダイヤグラム

$\ao{d}^3$ や $\ao{d}^8$ 電子配置は高スピン，低スピンの区別がなく，また他の電子配置よりもダイヤグラムがごちゃごちゃしていないので，スペクトル解析の練習題材としてよく使われます。$\ce{Ni^{II}}$ 錯体（$\ao{d}^8$）の吸収スペクトルと田辺・菅野ダイヤグラムから，吸収帯の帰属とラカーパラメータ $B$ の決定を行ってみましょう。下図は $\ce{Ni^{II}}$ のアクア錯体 $\ce{[Ni(OH2)6]^{2+}}$ の吸収スペクトルです。青で書いた数字は吸収帯のピークの波数です。強度が大きい低エネルギー側から $8,500$，$14,000$，$26,400\unit{\wn}$ の三つのピークを見ることができます。田辺・菅野ダイヤグラムを見ると，基底状態 $\irrep{^3A}{2g}$ からのスピン許容な遷移は三つあって，エネルギーが低い方から $\irrep{^3T}{2g}\leftarrow\irrep{^3A}{2g}$，$\irrep{^3T}{1g}(F)\leftarrow\irrep{^3A}{2g}$，$\irrep{^3T}{1g}(P)\leftarrow\irrep{^3A}{2g}$ であることは容易に分かります。

では，この錯体のラカーパラメータ $B$ はどのように求まるでしょうか。今のように帰属できた吸収帯が二つ以上ある場合は，そのエネルギーの比と田辺・菅野ダイヤグラムを比べることで $B$ を決めることができます。

$\ce{[Ni^{II}(OH2)6]^{2+}}$ の吸収スペクトル

$\ce{[Ni(OH2)6]^{2+}}$ のスペクトルで帰属されている三つの吸収帯のエネルギー比は，$14,000/8,500 = 1.65$，$26,000/14,000 = 1.86$，$26,000/8,500 = 3.06$ の組合せが可能ですが，一般的には比が大きい方が図の読み取りで誤差が小さくなると思われますので，ここでは $26,000/8,500 = 3.06$ を用いることにしましょう。すなわち，$\ao{d}^8$ 電子配置の田辺・菅野ダイヤグラムにおいて，$\irrep{^3T}{2g}\leftarrow\irrep{^3A}{2g}$ 遷移と $\irrep{^3T}{1g}(P)\leftarrow\irrep{^3A}{2g}$ 遷移のエネルギー比が $3.06$ になるような箇所を探せばよいわけです。

具体的には，例えばダイヤグラムの数値情報を持っているのであれば，コンピュータで条件を満たす箇所を求めるという方法もあると思いますが，ここでは（教育的配慮ということで）ローテクではありますが，田辺・菅野ダイアグラムに定規を当てて，長さの比が $3.06$ になる箇所を探しましょう。

下図で描いたように，横軸 $\Delta_\mathrm{O}/B = 9.5$ のときに条件を満たします（ローテクなので誤差はあります）。そしてこのとき，エネルギーが高い方の縦軸は $27$ と読み取れますので，$E/B = 27$ の $E$ に $26,000\unit{\wn}$ を代入して $B=963\unit{\wn}$ および $\Delta_\mathrm{O} = 9.5\times 963 = 9,150\unit{\wn}$ を得ます。縦軸を読む際はエネルギーが低い方の吸収帯の値を使っても構いません。$8,500\unit{\wn}$ でしたら縦軸 $E/B = 8.8$ くらいでしょうか。

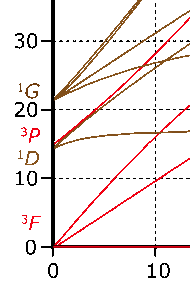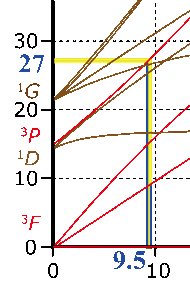
さて，今は三つある吸収帯のうちエネルギーが一番高い吸収帯と低い吸収帯を使い，中間の $14,000\unit{\wn}$ は使っていません。では，田辺・菅野ダイヤグラムで $26,000/8,500 = 3.06$ を満たす条件で，$14,000\unit{\wn}$ の吸収帯はうまく予測されるでしょうか。$E/B = 14,000/963 = 14.5$ 付近で $\irrep{^3T}{1g}(F)\leftarrow\irrep{^3A}{2g}$ 遷移と交差すれば良いわけですが，上図を見ると良い感じで予測されていることが分かるかと思います。

吸収スペクトルにはもう一つ，$15,400\unit{\wn}$ に強度が弱い遷移がありました。この吸収帯の帰属も田辺・菅野ダイヤグラムから行うことができます。$\irrep{^3T}{1g}(F)\leftarrow\irrep{^3A}{2g}$ よりも少し高エネルギー側に $\irrep{^1D}{}$ 項から生じる $\irrep{^1E}{g}$ 項がありますね。$15,400\unit{\wn}$ に観測される吸収帯は $\irrep{^1E}{g}(D)\leftarrow\irrep{^3A}{2g}$ のスピン禁制遷移であると帰属できます。