ヤーン・テラー効果

前節では，分裂した空の $\ao{d}$ 軌道を用意して，そこに電子を配置することで，錯体の電子状態を記述しました。さらに $\ao{d}$ 電子数が 4 ～ 7 個の場合にはスピン多重度が大きくなる高スピンと，小さくなる低スピンの二種類の状態を取りうることも学びました。そして，このような電子を配置する操作において，錯体の構造は変化せず，はじめに仮定した正八面体型などの構造を維持するというのが前節での立場でした。

しかし，例えば六配位錯体では，本当に常に正八面体型構造がエネルギー的に最も安定な構造でしょうか。実は違っていて，正八面体型構造から歪んだ構造をとる方がエネルギー的に安定になるメカニズムが知られており，それをヤーン・テラー効果（Jahn-Teller effect）といいます。もう少し丁寧に言うと，基底状態の電子配置が軌道の縮退を伴うとき，縮退が解けた状態の方がエネルギー的に安定であるため，錯体が歪んで対称性が低下する効果をヤーン・テラー効果と呼んでいます。

なぜ縮退が解けるとエネルギーが安定化するのでしょうか。典型例として，六配位正八面体型の $\ao{d}^9$ 錯体を考えます。高スピン，低スピンの区別はなく，基底電子配置は $\irrep{t}{2g}^6\irrep{e}{g}^3$ で表されます。ポイントは $\irrep{e}{g}$ 軌道に空きがあることで，分裂した空の $\ao{d}$ 軌道を考えると言っても，実際に電子が入らなければ，その分のエネルギー変化は生じません。$\irrep{e}{g}$ 軌道は $\ao{d}_{z^2}$ 軌道と $\ao{d}_{x^2-y^2}$ 軌道からなりますが，この二つの軌道は $z$ 軸方向の配位子が金属から遠ざかるという構造変化によって縮退が解けます。このとき，下図に示すように，エネルギーが低い側の軌道（図では $\ao{d}_{z^2}$ 軌道）に電子が二つ収まった状態の方が構造変化する前と比べて，全体のエネルギーは低くなります。この構造変化がヤーン・テラー効果です。もし，もう一つ電子が増えて $\ao{d}^{10}$ になると縮退が解けたことによって安定化する分と不安定化する分が相殺してトータルで変化なしとなりますので，ヤーン・テラー効果は生じません。

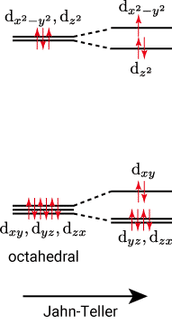
ヤーン・テラー効果

それでは $\ao{d}^8$ の場合はどうでしょうか。上図を見ると，不安定化した $\ao{d}_{x^2-y^2}$ 軌道から電子が一つ抜けるので，ヤーン・テラー効果がより強く現れると考えたくなりますが，$\ao{d}^8$ の場合の比較対象となるのは，縮退が解けていなくて（ヤーン・テラー効果がなくて）スピンが揃った三重項の状態と，縮退が解けてスピンが反対向きの一重項の状態です。構造変化による軌道エネルギーの変化だけを考えると，たしかにヤーン・テラー効果を考えた方がエネルギー的に安定化しますが，スピン多重度が異なり，多重度が大きい方が安定化しますので，両者のどちらの効果がより強く出るかという綱引きになって，結果としては通常ヤーン・テラー効果のような基底状態における構造変化は起こりません。

このように考えると，ヤーン・テラー効果が表れる基底電子配置は，$\grp{O}{h}$ 対称では $\ao{d}^1$，$\ao{d}^2$，$\ao{d}^4$（LS，HS），$\ao{d}^5$（LS），$\ao{d}^6$（HS），$\ao{d}^7$（LS，HS），$\ao{d}^9$ であり，また $\grp{T}{d}$ 対称では $\ao{d}^1$，$\ao{d}^3$，$\ao{d}^4$，$\ao{d}^6$，$\ao{d}^8$，$\ao{d}^9$ が該当します。しかし，$\grp{O}{h}$ 対称での $\grp{t}{2g}$ 軌道ならびに $\grp{T}{d}$ 対称でのすべての軌道は配位子方向に伸びていないため，ヤーン・テラー効果により得られるエネルギーの安定化は小さく，そのため構造変化も限定的になります。したがって，ヤーン・テラー効果によって比較的大きな構造変化が見られるのは $\grp{O}{h}$ 対称の $\ao{d}^4$（HS），$\ao{d}^7$（LS），$\ao{d}^9$ となります。