$\pH$ 計算の実際（緩衝液）

水に酸を加えれば酸性，塩基を加えれば塩基性になるのは当然ですが，酸や塩基を加えても素直に加えただけ酸性や塩基性にならない，すなわち溶液中のプロトン濃度の増減を自ら打ち消すような機能をもつ溶液があり，これを緩衝液（buffer）と呼んでいます。日常あまり意識することはありませんが，私たちの最も身近にある緩衝液は血液でしょう。私たちの血液は $\pH\,7.40$ 程度に保たれる緩衝液で，$\pH$ の変動はせいぜい $\pm 0.05$ 程度のようです。というのも血液の $\pH$ が $7.20$ を下回ると死に至ることもあるほどの人体に重篤な影響があるので，通常の環境では血液の $\pH$ はかなり高精度に保たれないと生命を維持することができません。もちろん能力には限界があるので，薬物中毒や病気などによって血液が酸性側に傾くような作用がはたらいている状態をアシドーシスといい，実際に $\pH$ が $7.35$ 未満になった状態は酸血症と診断されるそうです。

本節ではどのような溶液が緩衝作用を示すのか，そして緩衝液の $\pH$ はどのように決まるのかについて考察します。

共通イオン効果

緩衝液について考える前に，前提知識として共通イオン効果（common ion effect）について説明します。

具体例として酢酸 $\ce{AcOH}$ を考えます。酢酸は水中で次式に従い電離します。

$$\ce{AcOH <=> AcO- + H+}$$

電離度を $\alpha$ とすると，平衡状態において $\ce{AcOH}$ の濃度は $\Cacid(1-\alpha)$ であり，一方 $\ce{AcO-}$ と $\ce{H+}$ の濃度はどちらも $\Cacid\alpha$ です。$\Ka{} = 1.74\times 10^{-5}$ から酢酸の電離度を求めてみましょう。$\Cacid$ を具体的に定めないと式が煩雑になるので，とりあえず $\Cacid = 0.01\unit{M}$ としてみます。

\begin{align} &\Ka{} = \frac{\ce{[AcO-]}\ce{[H+]}}{\ce{[AcOH]}} = \frac{\Cacid\alpha^2}{1-\alpha} = 1.74\times 10^{-5}\\[10pt] &\alpha = 0.041 \end{align}

この濃度では溶かした酢酸のうちの約 $4\unit{\%}$ が電離していることになります。では次にこの溶液に（今の状態に加えて）酢酸イオンが追加で存在しているとしましょう。酢酸イオンという物質だけを追加するわけにはいかないので，具体的には酢酸ナトリウムのような完全電離する酢酸塩を加えることになりますが，ナトリウムイオンはこの先の議論には関わりません。溶液の酢酸ナトリウム濃度を $\Cbase$ とします。ここで元の酢酸の濃度は変わらず $\Cacid$ であることに注意してください。つまり，濃度 $\Cacid$ の酢酸溶液に，酢酸ナトリウム溶液を加えたのではなく，両者混合した段階で酢酸濃度が $\Cacid$，酢酸ナトリウム濃度が $\Cbase$ の溶液を考えます。ここでの共通イオンとは酢酸イオン $\ce{AcO-}$ のことです。

先ほどと同様にこの溶液の $\Ka{}$ を考えますが，酢酸ナトリウムからプロトンは出ませんので，プロトン濃度は酢酸溶液と同じく $\Cacid\alpha$ で表され，また電離していない酢酸として存在する分も上と同様に $\Cacid(1-\alpha)$ です。一方，酢酸イオンは酢酸由来の $\Cacid\alpha$ と酢酸ナトリウム由来の $\Cbase$ を合わせたものになりますので，$\Ka{}$ は次のように表されます。

$$\Ka{} = \frac{\ce{[AcO-]}\ce{[H+]}}{\ce{[AcOH]}} = \frac{(\Cacid\alpha + \Cbase)\Cacid\alpha}{\Cacid(1-\alpha)} = 1.74\times 10^{-5} \label{buffKa}$$

ここでも $\Cacid$ と $\Cbase$ を具体的に決めないと式が煩雑になるので，とりあえず上の例に合わせてどちらも $0.01\unit{M}$ にしてみます。

$$\alpha = 0.0017$$

この場合，酢酸濃度は等しいにもかかわらず，酢酸の電離度は $4.1\unit{\%}$ から $0.17\unit{\%}$ へと小さくなる（20 倍以上電離が抑制される）ことが分かります。このような弱電解質の水溶液にそれと共通のイオンを加えることによって，弱電解質の電離が抑えられる現象を共通イオン効果と呼んでいます。

緩衝液の $\pH$

緩衝液を理解する前提知識として共通イオン効果を学びましたが，実は既に緩衝液の話に足を半分以上突っこんだ状態です。と言うのも，上で挙げた酢酸と酢酸ナトリウムの混合水溶液というのは代表的な緩衝液の一つであるからです。本節ではこのように調製した緩衝液の $\pH$ について考えます。

鍵となるのは式(\ref{buffKa})で，プロトン濃度 $\ce{[H+]}$ が $\Cacid\alpha$ なので $\Ka{}$ は次のように書くことができます。

$$\Ka{} = \frac{\ce{[AcO-]}\ce{[H+]}}{\ce{[AcOH]}} = \frac{(\Cacid\alpha + \Cbase)\ce{[H+]}}{\Cacid(1-\alpha)} = \frac{(\ce{[H+]} + \Cbase)\ce{[H+]}}{\Cacid-\ce{[H+]}}$$

近似なしで解くのであればこの $\ce{[H+]}$ に関する 2 次方程式を解けば良いですが，今は弱酸を想定しているので $\alpha \ll 1$ かつ $\Cacid\alpha \ll \Cbase$ と考えてよいのであれば，方程式の次元は 1 次に下がります。

\begin{align} &\Ka{} = \frac{\Cbase\ce{[H+]}}{\Cacid}\\[10pt] &\Rightarrow \ce{[H+]} = \Ka{}\cdot\frac{\Cacid}{\Cbase}\\[10pt] &\Rightarrow \pH = \pKa{} + \log\frac{\Cbase}{\Cacid}\label{HHeq} \end{align}

式(\ref{HHeq})は ヘンダーソン・ハッセルバルヒの式（Henderson-Hasselbalch equation）と呼ばれるものですが，実は初出ではなくブレンステッド酸の学習の中で一度紹介しています。ただしこのときは式の活用法については説明しておりません。今がまさに活用のときです。

$2.00\times 10^{-2}\unit{M}$ 酢酸水溶液と $2.00\times 10^{-2}\unit{M}$ 酢酸ナトリウム水溶液を等量混合した水溶液の $\pH$ を求めます。$\pKa{}=4.76$ とします。

等濃度の水溶液を等量混合するので，$\Cacid$ と $\Cbase$ はどちらも $1.00\times 10^{-2}\unit{M}$ になりますが，必要なのはこれらの比で，具体的な濃度は使いません。

$$\pH = \pKa{} + \log\frac{\Cbase}{\Cacid} = 4.76 + \log 1 = 4.76$$

$\Cacid$ と $\Cbase$ の比が 1 であれば $\pH$ は $\pKa{}$ そのものになります。$1.00\times 10^{-2}\unit{M}$ 酢酸の $\pH$ は前に $3.38$ と求めてありますが，酢酸ナトリウムの存在によって酢酸の電離が抑制され，結果として $\pH$ の値が大きくなっていることが分かります。

$2.00\times 10^{-2}\unit{M}$ 酢酸水溶液と $1.00\times 10^{-2}\unit{M}$ 酢酸ナトリウム水溶液を等量混合した水溶液の $\pH$ を求めます。

先ほどより酢酸ナトリウムが少ない溶液になります。

$$\pH = \pKa{} + \log\frac{\Cbase}{\Cacid} = 4.76 + \log\frac{1}{2} = 4.46$$

緩衝液の機能

緩衝液の $\pH$ を求める方法について学びましたが，外的な変化があっても $\pH$ が変動しにくいというのが緩衝液の本来の機能ですので，緩衝液に酸や塩基を加えたときの $\pH$ 変化を考えなくてはいけません。ここでも緩衝液の具体例として酢酸と酢酸ナトリウムの混合水溶液を用い，外的要因として緩衝液に塩酸が加わる状況を考えてみましょう。

最初に場面設定ですが，$0.2\unit{M}$ 酢酸水溶液と $0.2\unit{M}$ 酢酸ナトリウム水溶液をそれぞれ $50\unit{mL}$ ずつ混合した $100\unit{mL}$ の緩衝液を考えます。つまりこの緩衝液の仕込みの濃度を考えると，$\Cacid = \Cbase = 0.1\unit{M}$ で $\pH\,4.76$ です。このとき溶液中に存在する $\ce{HOAc}$ と $\ce{OAc-}$ は共通イオン効果により酢酸の電離が抑制されることを踏まえると，どちらもほぼ $0.01\unit{mol}$ となります。

この緩衝液に塩酸 $\ce{HCl}$ を $1\times 10^{-3}\unit{mol}$ 分だけ加えてみましょう。簡単のため塩酸を加えたことによる体積変化は無視します。ちなみに純水 $100\unit{mL}$ に $1\times 10^{-3}\unit{mol}$ の $\ce{HCl}$ を加えると $\pH\,7$ から $\pH\,2$ へと大きく変化しますが，緩衝液では $\pH$ 変化がどの程度抑制されるでしょうか。加えられた $\ce{HCl}$ は塩基である酢酸イオン $\ce{OAc-}$ と反応します。

$$\ce{OAc- + HCl <=> HOAc + Cl-}$$

この反応により，溶液中では酢酸イオン $\ce{OAc-}$ が減少し，酢酸 $\ce{HOAc}$ が増加しますので，変化後の $\Cacid$ と $\Cbase$ を $\Cacid'$ と $\Cbase'$ と書くことにしましょう。

\begin{align} &\Cbase' = (0.01\unit{mol} - 0.001\unit{mol})/0.1\unit{L} = 0.09\unit{M}\\[7pt] &\Cacid' = (0.01\unit{mol} + 0.001\unit{mol})/0.1\unit{L} = 0.11\unit{M} \end{align}

したがって $\ce{HCl}$ を加えた後の緩衝液の $\pH$ は以下で求められます。

$$\pH = 4.76 + \log\frac{0.09}{0.11} = 4.67$$

純水に $\ce{HCl}$ を加えた場合と比べて，$\pH$ の変動が大きく抑制されていることが分かります。

緩衝能

ある緩衝液があるとき，当然ながら無限の能力を発揮してはくれませんので，どの程度の外的要因に対して，どの程度までの $\pH$ 変化で収まるかを知っておく必要があります。$\pH$ を $1$ 変化させるのに必要な $\Cacid$ または $\Cbase$ の変化量を緩衝液の緩衝能（buffer capacity）あるいは緩衝指数（buffer index）といいます。緩衝能 $\beta$ は次式で定義され，$\beta$ が大きいほど緩衝能が大きい（$\pH$ が変化しにくい）緩衝液となります。

$$\beta = -\frac{\partial\Cacid}{\partial(\pH)} = \frac{\partial\Cbase}{\partial(\pH)}$$

酸が加わると $\pH$ の変化量は負になりますが，$\beta$ を正値とするために中辺には負号がついています。また，着目しているもの以外は変化しないことを明示するために偏微分で表記しています。

$\beta$ を求めるには式(\ref{HHeq})を $\Cacid$ または $\Cbase$ で微分してその逆数を取ればよいのですが，どちらか一方を固定するよりは $\Cacid$ と $\Cbase$ の和が一定とした方が後で作成するプロットが見やすく便利です。そこで定数 $C_\mathrm{tot} = \Cacid + \Cbase$ を定義して式(\ref{HHeq})を書き直します。

$$\pH = \pKa{} + \log\frac{C_\mathrm{tot} - \Cacid}{\Cacid}$$

微分により $\beta$ を求めます。

$$\beta = -\frac{\partial\Cacid}{\partial(\pH)} = -\frac{1}{\frac{\partial(\pH)}{\partial\Cacid}} = \frac{\ln 10\,\Cacid(C_\mathrm{tot} - \Cacid)}{C_\mathrm{tot}}$$

$C_\mathrm{tot} = 0.2\unit{M}$ の場合の緩衝能を横軸を $\Cacid$，縦軸を $\beta$ としてプロットします。

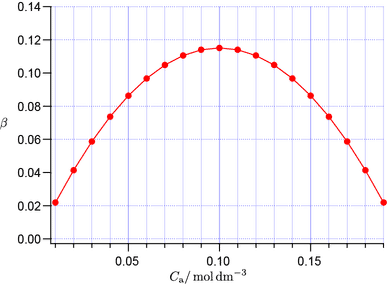
$\Cacid$ と緩衝指数 $\beta$ の関係

グラフより $\Cacid = 0.1\unit{M}$ すなわち $\Cacid$ と $\Cbase$ が $1:1$ のときに緩衝能 $\beta$ が最大となることが分かります。より一般性を持たせた書き方をすると，$C_\mathrm{tot}$ の値に関わらず $\Cacid=\frac{1}{2}C_\mathrm{tot}$ のとき $\beta$ は最大値をとります。上で酢酸と酢酸ナトリウムからなる緩衝液に $\ce{HCl}$ が加えられたときの $\pH$ 変化を求めました。同じ条件で $\ce{HCl}$ を増やしていったときの $\pH$ 変化をプロットします。

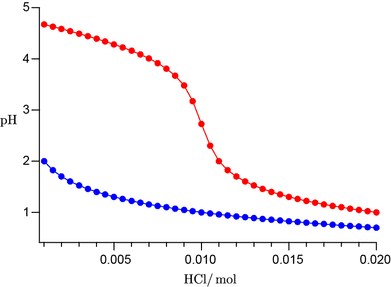
緩衝液に $\ce{HCl}$ を加えた際の $\pH$ 変化

（赤線：緩衝液，青線：純水）

赤線が緩衝液の場合，青線が純水の場合です。$\ce{HCl}$ を $0.01\unit{mol}$ 加えるとすべての $\ce{NaOAc}$ が中和に使われますので，このときの $\pH$ は酢酸溶液として計算しており，それ以降は塩酸と仮定して計算しています。どの程度の $\pH$ の変動を許容とするのかは用途によりますが，加える酸の量が酢酸ナトリウムの物質量に近づくと急激に緩衝機能が低下し，等量以降は緩衝機能はなくなり，実質，塩酸溶液として振る舞う（青のプロットを右に $0.01$ シフトすると赤に重なる）ことになります。緩衝溶液の $\pH$ は $\Cacid$ と $\Cbase$ の比で決まりますので，$0.001\unit{M}$ でも $0.1\unit{M}$ でも比が等しければ同じ $\pH$ の緩衝液が得られますが，緩衝液が外的要因にどの程度敏感であるかは比に加え，実際に存在する物質量 $C_\mathrm{tot}$ にも依存しますので，大きな外的要因に対しても安定した $\pH$ を維持したいのであれば，$\Cacid$ と $\Cbase$ を大きくする必要があります。

ここでは緩衝液に酸を加えた場合を考えましたが，塩基を加えた場合も同様の議論により $\ce{OAc-}$ が増加して $\ce{HOAc}$ が減少し，同様の結論が得られます。