$\pH$ 計算の実際

これまでは酸・塩基の概念を一般化し，有機溶媒中の化学反応であっても酸塩基反応として理解できるものがあるなど，酸・塩基の世界観を拡げる方向で話を進めてきました。一方，食品・医療などの応用的な現場では水溶液の $\pH$ というのは今でも重要な位置づけです。ある濃度の酸の水溶液があるとき，その $\pH$ は理論上どのように求められるでしょうか。狙った $\pH$ の水溶液を調製したいとき，どのようにすればよいでしょうか。あるいは，緩衝液の $\pH$ はどのように求まるでしょうか。本節では $\pH$ の計算法について紹介します。

初めにいくつか約束事です。水溶液の $\pH$ はプロトンの活量を $a_\ce{H+}$ として $-\log a_\ce{H+}$ で定義されますが，以下の議論では簡単のため活量係数を $1$ として $\pH$ が $-\log\ce{[H+]}$ で表されるものとします。参考として活量係数については資料を用意しました。また温度は $25\oC$ とし，このときの水のイオン積は $\Kw = 1.0\times 10^{-14}$ であるとします。仕込みの酸濃度，塩基濃度，塩濃度はそれぞれ $\Cacid$，$\Cbase$，$\Csalt$で表すことにします。仕込みの濃度（初期濃度ともいいます）とは，電離などを考えない調製した濃度そのものという意味です。濃度はモル濃度で表しますが，表記の簡単化のため，単位を $\mathrm{M}$ で表すことにします。

上の約束に従えば，一般論として溶液中のプロトン濃度が求まれば $\pH$ が求まります。プロトンを放出する候補は考えているブレンステッド酸自身と溶媒の水ですので，それぞれがどのくらいのプロトンを放出するかを考えれば良いことになります。

1 価の強酸水溶液

初めに 1 価の強酸を考えます。強酸というのは $\pKa{} < 0$ の酸のことをいいますが，$100\unit{\%}$ 電離しているとみなして問題ありません。具体的な 1 価の強酸というと塩酸や硝酸が代表的です。硫酸は 2 価ですのでこのカテゴリーには入りません。条件に応じて更に三つに場合分けします。

$\Cacid < 10^{-8}\unit{M}$ の場合

仕込みの酸濃度が $10^{-8}\unit{M}$ より小さいということは，これは極めて薄い酸です。このくらい薄くなると酸由来のプロトンよりも水の電離によるプロトンの方が圧倒的に多くなりますので，酸が $\pH$ に与える影響は無視できて，溶液は理論上 $\pH\,7$ に漸近します。ただし，このレベルの希薄さであると，空気中の二酸化炭素の影響の方が $\pH$ に与える影響が大きくなるので，空気中で実験をしている想定であれば，酸濃度と $\pH$ の関係という点からはあまり計算する意味のない濃度領域になります。

$\Cacid \approx 10^{-7}\unit{M}$ の場合

酸由来のプロトン $\ce{[H+]}_\mathrm{acid} = \Cacid$ と水由来のプロトン $\ce{[H+]_\ce{H2O}}$ の量が拮抗しているので，両方の寄与を考える必要があります。$\ce{[H+]_\ce{H2O}} = \ce{[OH-]_\ce{H2O}}$ ですので，水のイオン積 $\Kw$ は次式で表されます。

$$\Kw = \ce{[H+]}\ce{[OH-]} = (\Cacid + \ce{[H+]_{H_2O}})\ce{[H+]_{H_2O}} \label{Hwater}$$

これは $\ce{[H+]_\ce{H2O}}$ に関する 2 次方程式ですのでこれを解けば，全プロトン濃度は以下で求まります。

$$\ce{[H+]} = \Cacid + \ce{[H+]_\ce{H2O}}$$

$1.0\times 10^{-7}\unit{M}$ 塩酸水溶液の $\pH$ を求めます。式(\ref{Hwater})より $\ce{[H+]_\ce{H2O}} = 6.18\times 10^{-8}\unit{M}$ を得ます。よって以下により溶液の $\pH$ が求まります。

\begin{align} &\ce{[H+]} = 1.0\times 10^{-7} + 6.18\times 10^{-8} = 1.618\times 10^{-7} \\[10pt] &-\log\ce{[H+]} = 6.79 \end{align}

$\Cacid > 10^{-6}\unit{M}$ の場合

この条件では水の電離によるプロトン供給が $\pH$ に与える影響は無視できるので $\Cacid$ から直接 $\pH$ が求まります。

$2.0\times 10^{-3}\unit{M}$ 塩酸水溶液の $\pH$ を求めます。

$$-\log(2.0\times 10^{-3}) = 2.70$$

誤差の程度

上の議論を見ていただくと分かるように，近似を使わずいちばん真面目に求めているのが「$\Cacid \approx 10^{-7}\unit{M}$ の場合」ですが，一方いちばん簡単に計算できるのは「$\Cacid > 10^{-6}\unit{M}$ の場合」で示した方法です。実際両者の間でどの程度のずれが生じるのかを示したのが以下のグラフになります。

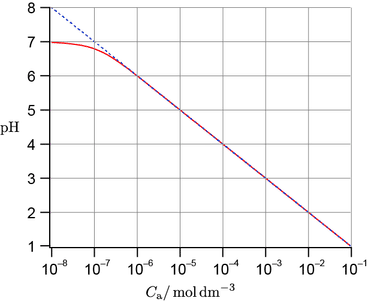
塩酸濃度と $\pH$ の関係

横軸は 1 価強酸の仕込みの濃度（対数軸）で縦軸が $\pH$ です。青の点線は「$\Cacid > 10^{-6}\unit{M}$ の場合」の方法で近似した結果，赤線が真面目に 2 次方程式を解いた結果です。これを見ると，$\Cacid > 10^{-6}\unit{M}$ では赤線と青点線がよく一致していることが分かります。また $\Cacid = 10^{-8}\unit{M}$ 付近で $\pH$ がほぼ $7$ となっていることも分かります。したがって（上で説明した通り）2 次方程式を真面目に解くのは $\Cacid \approx 10^{-7}\unit{M}$ の場合（より正確には $10^{-8}\unit{M}$ から $10^{-6}\unit{M}$ の範囲程度）だけで大丈夫です。

1 価の弱酸水溶液

弱酸水溶液では酸解離定数 $\Ka{}$ が一定に保たれます。この条件に加え，以下の二つの式を足がかりにプロトン濃度を求めます。

\begin{align} &\Cacid = \ce{[HA]} + \ce{[A-]} \label{massbalance}\\[10pt] &\ce{[H+]} = \ce{[OH-]} + \ce{[A-]} \label{chargebalance} \end{align}

式(\ref{massbalance})は質量均衡（mass balance）と呼ばれ，酸の仕込みの濃度は電離していない酸の濃度と電離した酸の濃度を足したものに等しいという当たり前のことを表した式です。式(\ref{chargebalance})は電荷均衡（charge balance）と呼ばれ，溶液全体の電荷はゼロになるという条件から得られるもので，これも当たり前といえば当たり前です。この二式を使って $\Ka{}$ を表します。

\begin{align} &\Ka{} = \frac{\ce{[H+]}\ce{[A^-]}}{\ce{[HA]}} = \frac{\ce{[H+]}\ce{[A^-]}}{\Cacid - \ce{[A-]}} = \frac{\ce{[H+]}(\ce{[H+]} - \ce{[OH-]})}{\Cacid - (\ce{[H+]} - \ce{[OH-]})} = \frac{\ce{[H+]}\left(\ce{[H+]} - \frac{\Kw}{\ce{[H+]}}\right)}{\Cacid - \left(\ce{[H+]} - \frac{\Kw}{\ce{[H+]}}\right)} \label{Kafull}\\[10pt] &\Rightarrow \ce{[H+]^3} + \Ka{}\ce{[H+]^2} - (\Cacid\Ka{}+\Kw)\ce{[H+]} - \Ka{}\Kw = 0 \label{Kafull3} \end{align}

$\Ka{}$ と $\Kw$ は定数，$\Cacid$ は設定値ですので，式(\ref{Kafull3})は $\ce{[H+]}$ に関する 3 次方程式になっています。したがって，式(\ref{Kafull3})を解けば近似なしで $\pH$ を求めることができますが，多くの場合は以下の近似を用いることで計算を簡単にすることができます。

$\ce{[H+]} \gg \ce{[OH-]}$ の場合

この場合 $\ce{[H+]} - \ce{[OH-]} \approx \ce{[H+]}$ として式(\ref{Kafull})を変形すると 2 次方程式に次数が下がるので解きやすくなります。

\begin{align} &\Ka{} = \frac{\ce{[H+]}^2}{\Cacid - \ce{[H+]}} \label{KaCaappr}\\[10pt] &\Rightarrow \ce{[H+]^2} + \Ka{}\ce{[H+]} - \Cacid\Ka{} = 0 \label{kacaka} \end{align}

なお条件の $\ce{[H+]} \gg \ce{[OH-]}$ ですが，$\pH$ 計算においては $\gg$ 記号は $5\unit{\%}$ 以下と言う認識が一般的です。つまり今の場合は $0.05\,\ce{[H+]} > \ce{[OH-]}$ が成り立っていれば条件を満たしていると考えてよいことになります。この条件は $\pH$ 換算で $0.02$ 程度以下の違いになります。一般的な $\pH$ 測定においての精度の限界が $0.02$ 程度（さらに言うと小数点以下 2 桁目の数字を正しく出すこと自体が実験的には結構大変）であるため，計算において $0.02$ 以上の精度を要求しても実用上の意味が小さいことから，近似の許容値としてこの値が受け入れられています。実際には条件を満たすかどうかは計算前にはわからないので，満たすと仮定して計算した結果が条件を満たしていればよし，満たしていなければ近似の程度を下げた式で計算しなおすといった進め方になります。

$\ce{[H+]} \gg \ce{[OH-]}$ かつ $\Cacid \gg \ce{[H+]}$ の場合

この条件が満たされるときは，式(\ref{KaCaappr})において $\Cacid - \ce{[H+]} \approx \Cacid$ と近似できますので，プロトン濃度は次式で求まります。

$$\ce{[H+]} = \sqrt{\Cacid\Ka{}} \label{caka}$$

式(\ref{caka})または電離度 $\alpha$ を用いた $\ce{[H+]}=\Cacid\alpha$ を公式として暗記している方もいると思いますが，あくまで近似式であって，使用に際しては近似が適用できるかどうかに注意を払う必要があります。

$\ce{[H+]} \gg \ce{[OH-]}$ が成り立たない場合

$\pKa{}$ が大きくて電離度が小さいと $\ce{[H+]} \gg \ce{[OH-]}$ の条件が成り立たないことがあります。このような場合でも $\Cacid \gg \ce{[H+]} - \ce{[OH-]}$ が成り立てば式(\ref{Kafull})を次のように変形できます。

\begin{align} &\Ka{} = \frac{\ce{[H+]}\ce{[A^-]}}{\ce{[HA]}} = \frac{\ce{[H+]}(\ce{[H+]} - \ce{[OH-]})}{\Cacid - (\ce{[H+]} - \ce{[OH-]})} = \frac{\ce{[H+]}(\ce{[H+]}-\ce{[OH-]})}{\Cacid} = \frac{\ce{[H+]^2} - \Kw}{\Cacid}\\[10pt] &\Rightarrow \ce{[H+]} = \sqrt{\Cacid\Ka{} + \Kw} \end{align}

$1.00\times 10^{-3}\unit{M}$ 酢酸水溶液の $\pH$ を求めます。ただし $\Ka{} = 1.74\times 10^{-5}$ とします。

まずは最もシンプルな式(\ref{caka})を使ってプロトン濃度を算出します。

$$\ce{[H+]} = \sqrt{1.75\times 10^{-8}} = 1.32\times 10^{-4}\unit{M}$$

これより求まる $\pH$ は $3.88$ ですが，このプロトン濃度は $0.05\,\Cacid = 5\times 10^{-5} > \ce{[H+]}$ を満たしていません。したがってこの $\pH$ をそのまま採用するのは危険（誤差が大きい）と判断し，改めて式(\ref{kacaka})を解くことにします。

$$\ce{[H+]} = \frac{-\Ka{}+\sqrt{\Ka{}^2 + 4\Cacid\Ka{}}}{2} = 1.23\times 10^{-4}\unit{M}$$

この結果は $0.05\,\ce{[H+]} > \ce{[OH-]} = \Kw/\ce{[H+]}$ の条件を満たしていますので，これより $\pH\,3.91$ と求まります。式(\ref{caka})を用いた場合とは $\pH$ が $0.03$ ほど異なりますので，実験的にも有意な差となります。

$1.00\times 10^{-2}\unit{M}$ 酢酸水溶液の $\pH$ を求めます。仕込みの濃度が上の例の 10 倍になっています。

式(\ref{caka})を使ってプロトン濃度を算出します。

$$\ce{[H+]} = \sqrt{1.74\times 10^{-7}} = 4.17\times 10^{-4}\unit{M}$$

$0.05\,\Cacid > \ce{[H+]}$ および $0.05\,\ce{[H+]} > \ce{[OH-]}$ の条件を満たしています。したがってこの結果から $\pH\,3.38$ と求まります。もちろん式(\ref{kacaka})を用いて解いても問題ありません。その場合 $\pH\,3.39$ が得られますが，差異は $0.02$ 以内に収まっていることが分かります。電離度は濃度が低くなるほど大きくなりますので，仕込みの濃度が 10 倍になっても $\pH$ 変化は $1$ にはなりません。

1 価の塩基水溶液

塩基の $\pH$ に関しても考え方は酸の場合と同じで，強塩基か弱塩基の違い，仕込みの濃度の違いによって場合分けします。酸の場合の $\Ka{}$ を $\Kb{}$ に，$\Cacid$ を $\Cbase$ に読み替えれば酸の場合と同じ方法で $\mathrm{pOH}$ が求まりますので，$\pH$ は $14-\mathrm{pOH}$ で得られます。ただし注意点として，塩基の場合は共役酸の $\Ka{}$ が与えられることが通常ですので，計算する際には変換が必要です。

$1.00\times 10^{-3}\unit{M}$ アンモニア水溶液の $\pH$ を求めます。ただし共役酸 $\ce{NH4+}$ の $\Ka{}$ は $5.6\times 10^{-10}$ とします。

$\Kb{} = \Kw/\Ka{} = 1.79\times 10^{-5}$ です。式(\ref{caka})の塩基版を使ってプロトン濃度を算出します。

$$\ce{[OH-]} = \sqrt{\Cbase\Kb{}} = \sqrt{1.79\times 10^{-8}} = 1.34\times 10^{-4}\unit{M}$$

$0.05\,\Cbase > \ce{[OH-]}$ の条件を満たしていませんので，式(\ref{kacaka})の塩基版で解きます。

$$\ce{[OH-]} = \frac{-\Kb{}+\sqrt{\Kb{}^2 + 4\Cbase\Kb{}}}{2} = 1.25\times 10^{-4}\unit{M}$$

$0.05\,\ce{[OH-]} > \ce{[H+]}$ の条件を満たしています。これより $\mathrm{pOH}\,3.90$ を得ますので $\pH\,10.1$ となります。