結晶場理論
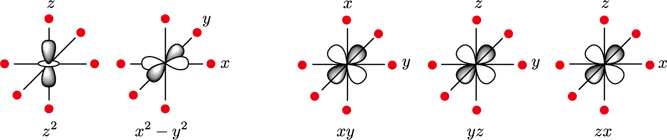
配位結合の形成により,金属イオンの五つの $\ao{d}$ 軌道に入った電子($\ao{d}$ 電子)と,配位子の非共有電子対は互いの距離が近づきます。その結果,負電荷どうしの静電反発によって,$\ao{d}$ 軌道のエネルギーが増加します。このような,配位子により作られる負電荷の環境を結晶場(crystal field)といいます。また,このような結晶場の考え方に基づいて金属イオンの状態を理解する理論を結晶場理論(crystal field theory)と呼んでいます。金属イオンの $\ao{d}$ 軌道は,配位子を有していなければ 5 重に縮退していますが,結晶場が存在すると,縮退が解けてエネルギーが分裂します。これを結晶場分裂(crystal field splitting)といいます。どのように縮退が解け,エネルギーが分裂するかは,結晶場をつくる配位子の数や,金属イオンを中心とした配位環境の対称性により変わります。
結晶場分裂
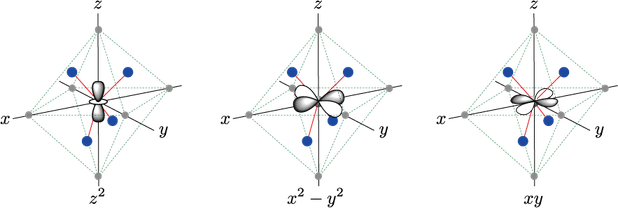
仮想的な状況ですが,ある量の負電荷が金属イオンを中心に球対称に接近してくる場合,すべての $\ao{d}$ 軌道のエネルギーは静電反発によって等しく上昇します。つまり,球対称な結晶場によって,$\ao{d}$ 軌道のエネルギーは上昇しますが,このとき軌道間の縮退は解けません。一方,六配位正八面体型の配位($\grp{O}{h}$ 対称)の場合,電荷の総量としては球対称場の場合と同じですが,それが下図の赤丸で示すように $x$,$y$,$z$ 軸方向の六つに集中して中心金属イオンに接近すると考えることができます。
正八面体型結晶場と $\ao{d}$ 軌道
この場合,$\ao{d}_{z^2}$ 軌道と $\ao{d}_{x^2-y^2}$ 軌道は軸方向に延びているため,これらの軌道にある電子は,近づく点電荷の負電荷との反発により,球対称場の場合と比べて,よりエネルギーが増大します。一方,$\ao{d}_{xy}$,$\ao{d}_{yz}$,$\ao{d}_{zx}$ の三つの軌道は,点電荷がない,軸と軸の間の方向に延びているため,球対称場の場合よりもエネルギーはむしろ小さくなります。これにより,$\grp{O}{h}$ 対称の結晶場においては,$\ao{d}$ 軌道は 2 重縮退した,エネルギーの高い $\ao{d}_{z^2}$,$\ao{d}_{x^2-y^2}$ 軌道($\irrep{e}{g}$ 軌道)と,3 重縮退したエネルギーの低い $\ao{d}_{xy}$,$\ao{d}_{yz}$,$\ao{d}_{zx}$ 軌道($\irrep{t}{2g}$ 軌道)とに分裂します。この様子を図示したのが下図になります。

正八面体型結晶場分裂
静電反発の詳しい計算を行うと,このときの分裂幅は $10Dq$ または $\Delta_\mathrm{O}$ で表され,球対称場と比べて,$\irrep{e}{g}$ 軌道は $6Dq$ だけエネルギーが高く,$\irrep{t}{2g}$ 軌道は $4Dq$ だけ低くなることが導かれます。$10Dq$ を結晶場分裂パラメータといいます。
四配位正四面体型の配位($\grp{T}{d}$ 対称)では,点電荷の接近方向と軸方向が一致しないため,構造をイメージしにくいですが,やはり点電荷の接近により,$\ao{d}$ 軌道は 2 重縮退した $\ao{d}_{z^2}$,$\ao{d}_{x^2-y^2}$ 軌道($\irrep{e}{}$ 軌道)と,2 重縮退した $\ao{d}_{xy}$,$\ao{d}_{yz}$,$\ao{d}_{zx}$ 軌道($\irrep{t}{2}$ 軌道)とに分裂します。ただし,この場合は $\irrep{t}{2}$ 軌道の方がエネルギーが高くなり,また点電荷の接近方向と軌道の方向が一致しないため,分裂は小さく,$Dq_\mathrm{tet}=-\frac{4}{9}Dq_\mathrm{oct}$ となります。
正四面体型結晶場

