偏微分と全微分

偏微分

1 変数関数についての微分は自然に多変数関数に拡張することができます。領域 $D\subset\mathbb{R}^2$ で定義された 2 変数関数 $z=f(x,y)$ が点 $(a,b)\in D$ において以下の極限値をもつとき，$f(x,y)$ は点 $(a,b)$ において $x$ に関して偏微分可能であると言い，この極限値である偏微分係数を $f_x(a,b)$ などと表します。$y$ についても同様で，$f_y(a,b)$ と表示します。

$$\lim_{h\rightarrow 0} \frac{f(a+h,b)-f(a,b)}{h}$$

$z = f(x,y)$ が $D$ の各点で $x$ に関して偏微分可能であるとき，$f(x,y)$ は $x$ に関して偏微分可能（$y$ についても同様）といい，$x$ と $y$ の両方に関して偏微分可能であるとき，この関数は（「～に関して」を付けずに）偏微分可能と言います。$z = f(x,y)$ が $x$ に関して偏微分可能であるような点 $(x,y)$ に $f_x(x,y)$ を対応させる関数を $z = f(x,y)$ の $x$ に関する偏導関数と言います。偏導関数には $f_x(x,y)$ の他，$\dfrac{\partial f}{\partial x}$ や $\left(\dfrac{\partial f}{\partial x}\right)_y$ のような表記法があります。特に最後の表記法は固定する変数を添え字で明記しており，関数 $f$ に定数を含む複数の文字が使われていた際にも，変数が $x$ と $y$ の二つであることが分かりやすいです。偏導関数を求めることを（$x$ に関して）偏微分すると言います。

関数が偏微分可能で，すべての偏導関数も連続ならば，その関数は $\pmb{C^1}$ 級関数であると言います。また，関数が 2 回偏微分可能（すべての 2 次偏導関数が存在する）で，すべての2 次偏導関数が連続ならば，その関数は $\pmb{C^2}$ 級関数であると言います。

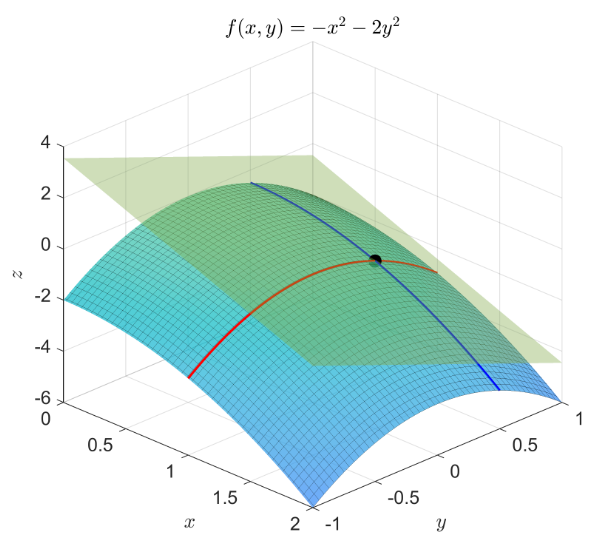
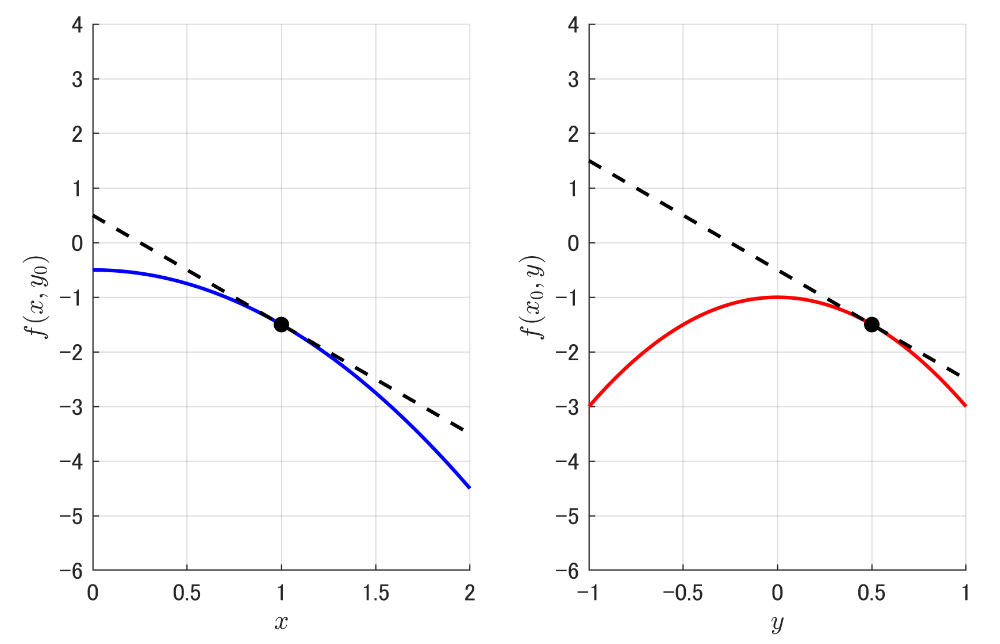
偏微分は多変数関数において，着目する一つの変数以外を定数であると見なして微分することに相当します。そのため操作としては通常の微分と変わりありません。下図は関数 $f(x,y)=-x^2-2y^2$ のグラフです。この関数を点 $(1, 0.5)$（グラフの黒点）で $x$ に関して偏微分するとは，点 $(1, 0.5)$ を通る $y$ 固定面（すなわち $y = 0.5$ の平面）とグラフとの交わり（青線）について $x=1$ での微分係数を求めることです。$y$ についても同様で，図では赤線で示しています。また偏導関数を求めるとは，青線（赤線）の関数を求めることに相当します。変数の数が 3 以上になるとグラフとしての表示は難しくなりますが，数学的な操作としては同様に偏微分を定義することができます。

1 変数関数の微分では「微分可能ならば連続」が成り立ちますが，多変数関数では「偏微分可能であっても連続とは限らない」という違いがあります。

全微分

偏微分は，ある特定の変数だけを変化させて関数の変化の割合を見るものでしたが，すべての変数が同時に変化するときに，それぞれの偏微分だけを個別に見ていても，関数の変化を正確に捉えることはできません。

多変数関数 $z = f(x, y)$ において，$x$ と $y$ の両方が微小に変化して $(x,y)$ から $(x + \Delta x,\, y + \Delta y)$ に移ったとき，$z$ の変化量 $\Delta z$ を偏微分係数を使って線形に近似できるのであれば，この右辺を 全微分と呼びます。

$$\Delta z \approx f_x(x, y) \Delta x + f_y(x, y) \Delta y$$

これは，$f(x, y)$ が点 $(x, y)$ のまわりで $x$ 軸方向の傾きと $y$ 軸方向の傾きを使ってよく近似できる一次式が存在するということを意味します。この近似の精度が高く，$\Delta x \to 0$，$\Delta y \to 0$ のときに近似誤差が無視できるほど小さくなる場合，関数 $f$ は点 $(x, y)$ において全微分可能であるといいます。

この式は微分の記号を使って次のように書き換えることもできます。

$$\diff z = \left(\frac{\partial f}{\partial x}\right)_y\diff x + \left(\frac{\partial f}{\partial y}\right)_x\diff y$$

ここで $\diff z$ は $f$ の全微分と呼ばれ，$\diff x$，$\diff y$ は $x$，$y$ の微小変化量です。上の図で示した関数 $f$ のグラフ上の点 $(x, y, f(x, y))$ における接平面（緑色）の方程式はこの全微分式に基づいて定まり，$f$ の局所的な線形近似を与えます。

関数が全微分可能であるための十分条件は，偏微分可能であり，かつすべての偏導関数が連続であることです。したがって，$C^1$ 級関数は全微分可能です。

高次偏微分と偏微分の順序

関数を複数回偏微分することを高次偏微分といいます。たとえば 2 変数関数 $f(x, y)$ に対し，まず $x$ に関して偏微分し，さらにもう一度 $x$ に関して偏微分する操作は，次のように表されます。

$$\frac{\partial^2 f}{\partial x^2} = \frac{\partial}{\partial x}\left( \frac{\partial f}{\partial x} \right)$$

同様に，最初に $x$，次に $y$ に関して偏微分する操作（交差項）は以下で表します。

$$\frac{\partial^2 f}{\partial y \partial x} = \frac{\partial}{\partial y}\left( \frac{\partial f}{\partial x} \right)$$

これに対して，$y$ で先に偏微分し，そのあとで $x$ に偏微分する操作は次の通りです。

$$\frac{\partial^2 f}{\partial x \partial y} = \frac{\partial}{\partial x}\left( \frac{\partial f}{\partial y} \right)$$

これらの操作は通常の偏微分を機械的に繰り返すだけで行うことができますが，ここで偏微分の順番を入れ替えても結果は同じになるのかという疑問が生じます。

この問いに対して，以下のシュワルツの定理が知られています。

関数 $f(x, y)$ が領域 $D$ において 2 回偏微分可能で，そのすべての 2 次偏導関数が連続であるとき（すなわち $f$ が $C^2$ 級関数のとき），次が成り立つ。

$$\frac{\partial^2 f}{\partial y \partial x} = \frac{\partial^2 f}{\partial x \partial y}$$

つまり，$C^2$ 級関数においては，偏微分の順番を入れ替えても結果は同じになります。逆に，関数が $C^2$ 級でなければ，この等式は一般には成り立たないことに注意が必要です。この性質は 3 変数以上や，より高次の偏微分に拡張しても同様に成り立ちます。$C^k$ 級関数（$k$ 回連続的に偏微分可能な関数）であれば，$k$ 回までの偏微分において順序を自由に入れ替えることができます。

化学の議論においては多くの多変数関数が $C^2$ 級の条件を満たします。したがって，シュワルツの定理のおかげで，多くの物理量や状態関数の微分操作において，偏微分の順番を交換した式変形が可能となります。