極座標

原子のような球状のものを対象とするときは，デカルト座標（座標）^[1]よりも極座標を用いた方が見通しが良くなります。

極座標表示

極座標とデカルト座標の関係は，表示したい点の原点からの距離が，軸から倒れる角度が，その倒れたベクトルが平面に影を作ったとき，影の軸からの角度がになります。変数の範囲は，はゼロから無限大，はゼロから，はゼロからとなります（またはからと定義してもよいです）。積分の際にをまで取ってしまうと二重カウントになってしまうので注意が必要です。

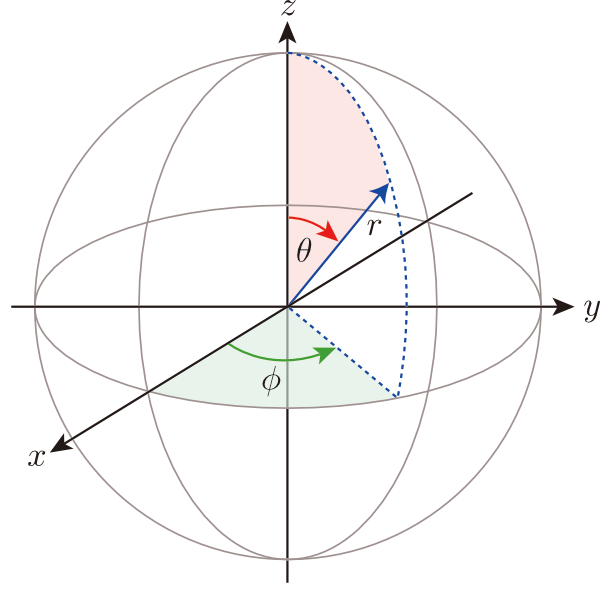
極座標とデカルト座標の変換には以下の式を使います。

やは，やの逆数ではなくて逆関数です。やで表すこともあります。紛らわしいですが Wikipedia に詳しく書いています。

極座標での積分

デカルト座標の積分を極座標に変換するには，が必要です。三重積分なので，積分記号を三つ重ねるのが本来の書き方ですが，自明の場合はわざわざ書かな場合も多いです。