ハメットの酸度関数の例
定義を再掲します。酸性度が大きくなると $\ce{[HInd+]}$ の割合が増えるので $H_0$ は小さくなります。$H_0$ は通常は負値をとりますので,$H_0$ が負に大きいほどプロトンを与える能力が大きい酸であるということになります。いくつか代表的な酸の $H_0$ を以下にまとめます。より詳しい表は資料のハメットの酸度関数にまとめました。
塩酸
市販の濃塩酸はおよそ $35$~$37\unit{\%}$ の濃度です。表中の $-\log\Cacid$ は低濃度では $\pH$ であり $H_0$ と一致することが分かります。
| 質量パーセント | $\Cacid/\molL$ | $H_0$ | $-\log\Cacid$ |
|---|---|---|---|
| $0.1$ | $0.027$ | $1.56$ | $1.57$ |
| $0.5$ | $0.137$ | $0.84$ | $0.86$ |
| $1$ | $0.274$ | $0.52$ | $0.56$ |
| $10$ | $2.87$ | $-0.98$ | $-0.46$ |
| $20$ | $6.03$ | $-2.10$ | $-0.78$ |
| $36$ | $11.7$ | $-4.14$ | $-1.07$ |
フッ化水素
「ハロゲン化水素はいずれも強酸であるが,フッ化水素 $\ce{HF}$ だけは弱酸である」と記憶している方もいるかと思います。しかしこの認識は間違いで,高校の教科書をよく見てみると「フッ化水素の水溶液であるフッ化水素酸は弱酸」と書いてあるはずです。たしかに希薄な水溶液ではフッ化水素は弱酸ですが,濃度が高くなると酸性度は高くなります。超酸の例としてフルオロアンチモン酸を学習しましたが,このときに用いるフッ化水素は液化した純粋な $\ce{HF}$ であり,水溶液ではありません。
下のグラフは硫酸(実線)とフッ化水素酸(破線)の水溶液濃度と $H_0$ の関係を示したものです(H. H. Hyman, M. Kilpatrick, J. J. Katz J. Am. Chem. Soc., 1957, 79, 3668-3671. より引用)。上の塩酸の $H_0$ と比べると,たしかに同濃度の塩酸よりは $H_0$ が大きい(酸性度が小さい)ですが,濃度が高くなるにつれて $H_0$ は小さくなり,$100\unit{\%}$ では $H_0 = -10.2$ と報告されています。
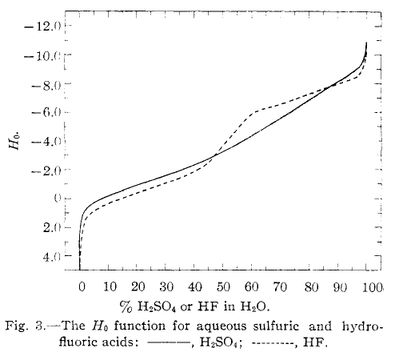
| 質量パーセント | $H_0$ |
|---|---|
| $2.07$ | $1.33$ |
| $9.81$ | $0.38$ |
| $25.3$ | $-0.82$ |
| $48.7$ | $-3.55$ |
| $80.9$ | $-7.52$ |
| $90.2$ | $-8.17$ |
| $100 $ | $-10.2$ |
硫酸
超酸の定義が「$100\unit{\%}$ 硫酸よりもプロトンを与える能力が高い酸」ですので,硫酸の $H_0$ を知っておくことは大切です。$100\unit{\%}$ 硫酸の $H_0$ は $-11.94$ と報告されていますので,$H_0$ が $-12$ 以下の物質が超酸と分類されます。いわゆる濃硫酸と呼ばれるものは $98\unit{\%}$ くらい,車のバッテリー(鉛蓄電池)に使われているものが $30\unit{\%}$ くらいの濃度です。濃硫酸は実は弱酸であるというような言い方をされることがありますが,(水が少ないので)完全電離しないと言う意味であって,プロトンを与える能力が小さいという意味ではないので注意が必要です。
| 質量パーセント | $H_0$ |
|---|---|
| $2$ | $0.53$ |
| $4$ | $0.2$ |
| $6$ | $-0.02$ |
| $8$ | $-0.2$ |
| $10$ | $-0.35$ |
| $30$ | $-1.73$ |
| $50$ | $-3.3$ |
| $80$ | $-7.46$ |
| $98$ | $-10.43$ |
| $100$ | $-11.94$ |
超酸
| $H_0$ | ||
|---|---|---|
| フルオロアンチモン酸 | $50\unit{\%}\,\ce{HF} + 50\unit{\%}\,\ce{SbF5}$ | $-31.3$ |
| マジック酸 | $25\unit{\%}\,\ce{SbF5} + 75\unit{\%}\,\ce{HSO3F}$ | $-21.5$ |
| フルオロ硫酸 | $\ce{HSO3F}$ | $-15.1$ |
| 過塩素酸 | $\ce{HClO4}$ | $-13.0$ |

