ハメットの酸度関数

前節までで水溶液の $\pH$ の求め方を様々な状況に場合分けして学びました。$\pH$ を求める際には多くの場合，酸・共役酸の $\pKa{}$ を用います。しかし酸解離定数 $\Ka{}$ は次式で示すように溶媒である水の活量 $a_\ce{H2O}$ を $1$ としたときの定数ですから，逆に言うと $a_\ce{H2O}$ が $1$ とはみなせない（溶媒の水が大過剰とは言えない，あるいはそもそも水が存在しない）ような溶液ではこれまでの方法で $\pH$ を求めて，酸や塩基の強さを比較することはできません。

$$\Ka{} = \frac{a_{\ce{H3O+}}\cdot a_{\ce{A-}}}{a_{\ce{HA}}\cdot a_{\ce{H2O}}} \approx \frac{[\ce{H3O+}][\ce{A-}]}{[\ce{HA}]} \equiv \frac{[\ce{H+}][\ce{A-}]}{[\ce{HA}]} \label{Kadef}$$

また，水溶液中では水平化効果によって強酸や強塩基水溶液の $\pH$ が取りうる範囲には限界があることも学びましたが，これは見方を変えると，酸や塩基が本来もつプロトンを与える（受け取る）能力を，溶媒である水が覆い隠してしまっているということですから，水溶液ではなく，物質としての酸や塩基そのものが本来持つ能力を評価するには $\pH$ 以外の別の指標が必要となります。

具体的には，濃厚溶液，超酸・超塩基，非水溶媒系といった条件では溶液の $\pH$ により酸や塩基の強さを比較することは困難です。そこでこのような状況であっても適用できる指標として知られているハメット（Hammett）により提唱されたハメットの酸度関数について説明します。以下簡単のため，酸についてのみ考えますが塩基の場合も同様の議論が可能です。

指示薬

初めに酸性度を求めたい酸を $\ce{HA}$ で表し，$\ce{HA}$ と指示薬（indicator）との反応を考えます。指示薬という言葉の意味は後で明らかになりますが，指示薬の実体は $\ce{HA}$ からプロトンを受け取るブレンステッド塩基です。ですので $\ce{B}$ で表してもよいのですが，ここでは指示薬であることを明示するために $\ce{Ind1}$ で表します。添え字の $1$ は後で別の指示薬 $2$ が出てくることの伏線です。指示薬は弱い塩基であり，ごく少量だけ存在するとします。

$$\ce{HA + Ind1 <=> A- + HInd1+}$$

指示薬 $\ce{Ind1}$ の共役酸である $\ce{HInd1+}$ の $\Ka{}$ を考えます。

\begin{align} &\ce{HInd1+ <=> H+ + Ind1} \\[10pt] &\Ka{}(\ce{HInd1+}) = \frac{a_\ce{H+}\cdot a_\ce{Ind1}}{a_\ce{HInd1+}} = \frac{\ce{[H+]}\ce{[Ind1]}}{\ce{[HInd1+]}}\cdot\frac{\gamma_\ce{H+}\cdot\gamma_\ce{Ind1}}{\gamma_\ce{HInd1+}} \label{kahind1} \end{align}

ここで $\gamma$ は各化学種の活量 $a$ とモル濃度を結ぶ活量係数で，例えば $a_\ce{H+} = \gamma_\ce{H+}\ce{[H+]}$ のように表されることは既に説明してあります。これまでは活量係数は $1$ であると近似して $a_\ce{H+}\approx\ce{[H+]}$ などとみなしてきましたが，ここでは活量係数を無視せずに考えます。式(\ref{kahind1})より $\ce{HInd1+}$ の $\pKa{}$ は次のように表されます。

$$\pKa{}(\ce{HInd1+}) = -\log a_\ce{H+} + \log\frac{\ce{[HInd1+]}}{\ce{[Ind1]}} + \log\frac{\gamma_\ce{HInd1+}}{\gamma_\ce{Ind1}} \label{pkaind1}$$

次に，まったく同様の考え方で，別の指示薬 $\ce{Ind2}$ を考え，$\ce{Ind2}$ の $\pKa{}$ を求めます。

$$\pKa{}(\ce{HInd2+}) = -\log a_\ce{H+} + \log\frac{\ce{[HInd2+]}}{\ce{[Ind2]}} + \log\frac{\gamma_\ce{HInd2+}}{\gamma_\ce{Ind2}} \label{pkaind2}$$

当然ながら式(\ref{pkaind1})と式(\ref{pkaind2})は添え字が違うのみで他はまったく同じです。ここで右辺第一項の $-\log a_\ce{H+}$ に注目してください。この項は溶液中のプロトンの活量のみに依存しており，指示薬の種類にはよらないため，酸 $\ce{HA}$ が持つ固有の性質であると考えることができます。そこで，ある同じ酸（同じ $a_\ce{H+}$ を持つ）に異なる指示薬である $\ce{Ind1}$ と $\ce{Ind2}$ を溶かしたときの $-\log a_\ce{H+}$ は等しいとして式(\ref{pkaind1})と(\ref{pkaind2})を引き算すると次の関係を得ます。

$$\pKa{}(\ce{HInd1+}) - \pKa{}(\ce{HInd2+}) = \log\frac{\ce{[HInd1+]}}{\ce{[Ind1]}} - \log\frac{\ce{[HInd2+]}}{\ce{[Ind2]}} + \log\left(\frac{\gamma_\ce{HInd1+}}{\gamma_\ce{Ind1}}\cdot\frac{\gamma_\ce{Ind2}}{\gamma_\ce{HInd2+}}\right) \label{pkaind12}$$

ハメットの酸度関数

ここまでで指示薬の電離挙動を定式化しました。次に式(\ref{pkaind12})の右辺第三項に着目します。この項は指示薬とその共役酸の活量係数の比を 2 種類の指示薬について求め，これらを割り算している（逆数をかけている）ことになります。 2 種類の指示薬は異なる化合物ですので，その活量係数は厳密には異なりますが，分子の電荷や極性，濃度といった活量係数に影響を与えそうな因子をできるだけ揃えた指示薬どうし（以下では似た指示薬と表記します）では $\gamma_\ce{HInd1}\approx\gamma_\ce{HInd2}$，$\gamma_\ce{Ind1}\approx\gamma_\ce{Ind2}$ と近似してもよさそうです。すると右辺第三項はゼロとなりますので，式(\ref{pkaind12})は以下のようになります。

\begin{align} &\pKa{}(\ce{HInd1+}) - \pKa{}(\ce{HInd2+}) = \log\frac{\ce{[HInd1+]}}{\ce{[Ind1]}} - \log\frac{\ce{[HInd2+]}}{\ce{[Ind2]}} \label{pka1ind12}\\[10pt] &\Rightarrow \pKa{}(\ce{HInd1+}) - \log\frac{\ce{[HInd1+]}}{\ce{[Ind1]}} = \pKa{}(\ce{HInd2+}) - \log\frac{\ce{[HInd2+]}}{\ce{[Ind2]}} \label{pkaind12sim} \end{align}

式(\ref{pkaind12sim})が意味するところは，似た指示薬どうしであれば $\pKa{}$ から指示薬 $\ce{Ind}$ とその共役酸 $\ce{HInd+}$ の存在比の対数を引いたものは指示薬の種類によらず一定になるということです。そこでこれをハメットの酸度関数（Hammett acidity function）$H$ と定義します。

$$H \equiv \pKa{}(\ce{HInd+}) - \log\frac{\ce{[HInd+]}}{\ce{[Ind]}} \label{hammett1}$$

これより $\ce{HInd+}$ の $\pKa{}$ と，溶液中における $\ce{HInd+}$ と $\ce{Ind}$ の存在比がわかれば $H$ を実験的に決定することができます。$\pKa{}$ についてはひとまず置いておいて，$\ce{HInd+}$ と $\ce{Ind}$ の存在比について考えます。溶液中の化学種の存在量を知る実験手法はいくつかありますが，いちばん典型的な手法として比色分析，すなわち $\ce{HInd+}$ と $\ce{Ind}$ とで異なる色を持つものを指示薬として採用し，溶液の色の分析によって存在比や存在量を知る方法があります。本節の最初に指示薬という名称を与えたのはこれが理由です。

式(\ref{hammett1})は式(\ref{pkaind1})を使って変形できます。

$$H = \pKa{}(\ce{HInd+}) - \log\frac{\ce{[HInd+]}}{\ce{[Ind]}} = -\log a_\ce{H+} - \log\frac{\gamma_\ce{HInd+}}{\gamma_\ce{Ind}}$$

溶液を水で希釈すると活量係数は $1$ に近づきますので，希薄な酸では $H$ は $-\log a_\ce{H}$ に近づきますが，これは $\pH$ の定義そのものですので，ハメットの酸度関数 $H$ は希薄な領域では $\pH$ とスムーズに接続してくれる，酸の強度を表すのに都合の良い指標であることが分かります。

なおハメットの酸度関数を求める際の指示薬の候補にはいくつかのタイプがあって，どのタイプの指示薬を使って求めた $H$ なのかを添え字で表現することになっています。いちばん一般的なのは，中性すなわち電荷がゼロの塩基を指示薬として用いる方法で，この場合は電荷ゼロの 0 をつけて $H_0$ と表します。これまでの議論では指示薬は $\ce{Ind}$ で表し中性であることを暗に示してきました。よってハメットの酸度関数の定義を改めて書くと以下のようになります。

$$H_0 \equiv \pKa{}(\ce{HInd+}) - \log\frac{\ce{[HInd+]}}{\ce{[Ind]}} \label{hammettdef}$$

指示薬の $\pKa{}$

上で「$\pKa{}$ と，溶液中における $\ce{HInd+}$ と $\ce{Ind}$ の存在比がわかれば」とさらりと書きましたが，特に前半の $\pKa{}$ を知るのは結構大変です。式(\ref{pkaind1})に戻ります。式(\ref{pkaind1})において水で希釈すれば $\gamma$ は $1$ に近づきますが，$\Ka{}$ は定数ですので希釈（酸 $\ce{HA}$ の仕込みの濃度 $\Cacid$ をゼロに近づける）しても変わりません。よって $\pKa{}(\ce{HInd1+})$ は次式によって表すこともできます。

$$\pKa{}(\ce{HInd+}) = \lim_{\Cacid\rightarrow 0}\left[-\log \ce{[H+]} + \log\frac{\ce{[HInd+]}}{\ce{[Ind]}}\right] \label{limpkaind}$$

$\ce{HA}$ が 1 価の強酸であれば完全電離しますので $\Cacid = \ce{[H+]} + \ce{[HInd+]}$ となり，$\ce{[HInd+]}$ を（比色分析などで）実験的に求めることで $\ce{[H+]}$ が見積もられ，式(\ref{limpkaind})右辺[　]の中が求まります。したがって，横軸を $\Cacid$，縦軸を式(\ref{limpkaind})の[　]の中としたプロットを酸濃度を色々に変えて作成し，それを $\Cacid = 0$ に外挿した値を見積もれば，それが $\pKa{}(\ce{HInd+})$ となります。下の図は過塩素酸中で三つの指示薬について $\pKa{}$ を求めた実験のプロットです（M. A. Paul, F. A. Long Chem. Rev., 1957, 57, 1-45. より引用）。

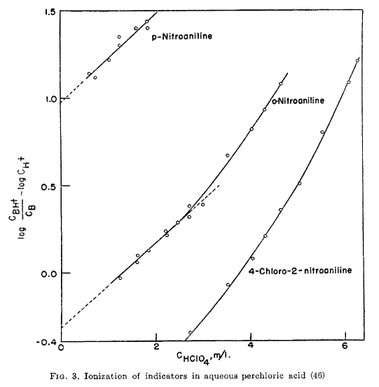
上記の方法で $\pKa{}$ を決められるのは指示薬が強い塩基の場合で，弱い塩基では希釈したときに十分に $\ce{[HInd+]}$ が生じないため $\pKa{}$ の決定は困難です。ところが，いざ指示薬を使うときというのは，普通はプロトンを与える能力が大きい酸の $H_0$ を求めるときですので，指示薬が強い塩基だとすべてが共役酸 $\ce{[HInd+]}$ になってしまって，$\ce{[HInd+]}$ と $\ce{[Ind]}$ の比を求めることができません。よって弱い塩基の指示薬について $\pKa{}$ を求める必要があります。

そこで再び式(\ref{pka1ind12})に着目します。式(\ref{pka1ind12})の右辺は（溶液の酸性度と指示薬の塩基性の強さのバランスが良ければ）実験的に決められます。よって，もし左辺の $\pKa{}(\ce{HInd1+})$ が既知であれば $\pKa{}(\ce{HInd2+})$ を求めることができますが，この $\pKa{}(\ce{HInd1+})$ に上の方法で求めた値を採用すればよさそうです。実際にはいくつもの指示薬を用意してこのような関係を複数見積もり，結果をフィッティングすることによって $\pKa{}$ を求めることになります。