生成定数

本節では金属イオンと配位子との間の平衡について考察します。水溶液中の水和した金属イオン $\ce{M(OH2)_n}$ に，$n$ 個の配位子 $\ce{L}$ が置換して $\ce{ML_n}$ が生成する反応を考えてみましょう。この反応は，$\ce{L}$ が順番に置換していく $n$ 段階の反応に分けて考えることができます。

\begin{alignat}{5} &\ce{M} &+\ &\ce{L <=> ML} & \quad & K_\mathrm{f1} = \frac{\ce{[ML] }}{\ce{[M][L] }} & \quad & \beta_1 = K_\mathrm{f1} &\quad & = \frac{\ce{[ML] }}{\ce{[M][L] }} \label{MLML} \\[10pt] &\ce{ML} &+\ &\ce{L <=> ML_2} & & K_\mathrm{f2} = \frac{\ce{[ML_2]}}{\ce{[ML][L] }} & & \beta_2 = K_\mathrm{f1}K_\mathrm{f2} & & = \frac{\ce{[ML_2]}}{\ce{[M][L]^2}} \\[10pt] &\ce{ML_2} &+\ &\ce{L <=> ML_3} & & K_\mathrm{f3} = \frac{\ce{[ML_3]}}{\ce{[ML_2][L] }} & & \beta_3 = K_\mathrm{f1}K_\mathrm{f2}K_\mathrm{f3} & & = \frac{\ce{[ML_3]}}{\ce{[M][L]^3}} \\[10pt] &\ce{ML_{n-1}}\ &+\ &\ce{L <=> ML_n} & & K_{\mathrm{f}n} = \frac{\ce{[ML_n]}}{\ce{[ML_{n-1}][L]}} & & \beta_n = K_\mathrm{f1}K_\mathrm{f2}\cdots K_{\mathrm{f}n} & & = \frac{\ce{[ML_n]}}{\ce{[M][L]^n}} \label{MLn1LMLn} \end{alignat}

$K_\mathrm{f1}$，$K_\mathrm{f2}$，$\cdots$，$K_{\mathrm{f}n}$ は各反応段階の逐次生成定数 $K_\mathrm{f}$ であり，$\beta_1$，$\beta_2$，$\cdots$，$\beta_n$ は，その段階までの全生成定数です。$K_\mathrm{f}$ が大きいほど，その段階での生成物が熱力学的に安定（stable）であることを意味します。アクア配位子の置換反応についての $K_\mathrm{f}$ と $\beta$ の例を以下に示します。

	$K_\mathrm{fi}$	$\beta_i$		$K_\mathrm{fi}$	$\beta_i$
$\ce{[Cu(OH2)4]^{2+} + NH3}$	$K_\mathrm{f1}=10^{4.3}$	$\beta_1=10^{4.3}$	$\ce{[Cd(OH2)4]^{2+} + NH3}$	$K_\mathrm{f1}=10^{2.65}$	$\beta_1=10^{2.65}$
	$K_\mathrm{f2}=10^{3.3}$	$\beta_2=10^{7.6}$		$K_\mathrm{f2}=10^{2.10}$	$\beta_2=10^{4.75}$
	$K_\mathrm{f3}=10^{2.9}$	$\beta_3=10^{10.5}$		$K_\mathrm{f3}=10^{1.44}$	$\beta_3=10^{6.19}$
	$K_\mathrm{f4}=10^{2.3}$	$\beta_4=10^{12.8}$		$K_\mathrm{f4}=10^{0.93}$	$\beta_4=10^{7.12}$
$\ce{[Hg(OH2)6]^{2+} + Cl-}$	$K_\mathrm{f1}=10^{6.7}$	$\beta_1=10^{6.7}$	$\ce{[Cd(OH2)4]^{2+} + Br-}$	$K_\mathrm{f1}=10^{1.56}$	$\beta_1=10^{1.56}$
	$K_\mathrm{f2}=10^{6.5}$	$\beta_2=10^{13.2}$		$K_\mathrm{f2}=10^{0.54}$	$\beta_2=10^{2.10}$
	$K_\mathrm{f3}=10^{0.9}$	$\beta_3=10^{14.1}$		$K_\mathrm{f3}=10^{0.06}$	$\beta_3=10^{2.16}$
	$K_\mathrm{f4}=10^{1.0}$	$\beta_4=10^{15.1}$		$K_\mathrm{f4}=10^{0.37}$	$\beta_4=10^{2.53}$

ここからどのような情報が得られるでしょうか。配位子 $\ce{L}$ の金属イオンに対する配位や，その逆反応である解離が単純に確率的に起こると仮定すると，$K_\mathrm{f}$ は極端なステップのない $K_\mathrm{f1}>K_\mathrm{f2}>K_\mathrm{f3}>\cdots >K_{\mathrm{f}n}$ の大小関係になります。上の表に示した例の中では $\ce{[Cu(OH2)4]^{2+}}$ の $\ce{OH2}$ が $\ce{NH3}$ に置換する反応において，この大小関係が分かりやすく現れています。

一方，確率に基づく予想値とは異なる $K_\mathrm{f}$ の関係が生じる場合もあります。そのような場合は，単純な確率に基づく反応以外の要因が含まれていると考えられるわけで，錯体の電子状態や化学構造の変化などと生成定数とが密接に関係している場合もあります。例えば以下に示すように，$\ce{[Fe(OH2)6]^{2+}}$ の $\ce{OH2}$ がbipyridine (bpy)に置換される反応では，$K_\mathrm{f3}$ が $K_\mathrm{f2}$ に比べて圧倒的に大きくなっています。これは，$\ce{[Fe(bpy)2(OH2)2]^{2+}}$ では高スピン状態 $\irrep{t}{2g}^4\irrep{e}{g}^2$ の電子状態であった $\ce{Fe(II)}$ が，$\ce{[Fe(bpy)3]^{2+}}$ になると，低スピン状態の $\irrep{t}{2g}^6$ へと電子状態が変わることにより，配位子場安定化エネルギーLFSEが大きくなるためです。

\begin{alignat}{2} &\ce{[Fe(OH2)6]^{2+}(aq) + bpy(aq) <=> [Fe(bpy)(OH2)4]^{2+}(aq) + 2H2O(l)} & & \log K_\mathrm{f1} = 4.2 \\[10pt] &\ce{[Fe(bpy)(OH2)4]^{2+}(aq) + bpy(aq) <=> [Fe(bpy)2(OH2)2]^{2+}(aq) + 2H2O(l)} & & \log K_\mathrm{f2} = 3.7 \\[10pt] &\ce{[Fe(bpy)2(OH2)4]^{2+}(aq) + bpy(aq) <=> [Fe(bpy)3]^{2+}(aq) + 2H2O(l)} & \qquad & \log K_\mathrm{f3} = 9.3 \end{alignat}

一方，上の表にもある通り，$\ce{[Hg(OH2)6]^{2+}}$ のアクア配位子が $\ce{Cl-}$ と置換する反応を見ると，$K_\mathrm{f3}$ が $K_\mathrm{f2}$ と比べて極端に小さいことが分かります。このような場合は，三つ目のクロリド配位子が置換することに抵抗するような，何かしらの特別なことが起こっているなと察することができて，実際この場合は，$\ce{[HgCl2(OH2)4]}$ に $\ce{Cl-}$ が配位する際に，六配位から四配位に錯体の構造が変わることが要因であると考えられます。

\begin{alignat}{2} &\ce{[Hg(OH2)6]^{2+}(aq) + Cl-(aq) <=> [HgCl(OH2)5]^+(aq) + H2O(l)} & & \log K_\mathrm{f1} = 6.7 \\[10pt] &\ce{[HgCl(OH2)5]^+(aq) + Cl-(aq) <=> [HgCl2(OH2)4](aq) + H2O(l)} & & \log K_\mathrm{f2} = 6.5 \\[10pt] &\ce{[HgCl2(OH2)4](aq) + Cl-(aq) <=> [HgCl3(OH2)]^-(aq) + 3H2O(l)} & \qquad & \log K_\mathrm{f3} = 0.9 \end{alignat}

金属 $\ce{M}$ の多段階置換反応において，全生成定数 $\beta_1$，$\beta_2$，$\cdots$，$\beta_n$ が分かれば，溶液中の配位子 $\ce{L}$ の濃度に対して，その溶液中に含まれる各置換体の存在比を求めることができます。式(\ref{MLML})～(\ref{MLn1LMLn})より，溶液中の金属を含むすべて化学種を合わせた全濃度 $\mathrm{[M_{tot}]}$ および，置換体 $\ce{ML_x}$ の濃度 $\ce{[ML_x]}$ はそれぞれ以下で表されます。

\begin{alignat}{2} &\mathrm{[M_{tot}]} &=& \ \ce{[M]} + \ce{[ML]} + \ce{[ML_2]} + \cdots + \ce{[ML_n]} \nonumber \\[10pt] & &=& \ \ce{[M]} + \beta_1\ce{[M][L]} + \beta_2\ce{[M][L]^2} + \cdots + \beta_n\ce{[M][L]^n} \\[10pt] &\ce{[ML_x]} &=& \ \beta_x\ce{[M][L]}^x \end{alignat}

これより，溶液中の $\ce{ML_x}$ の存在比 $\alpha_x$ は次のように表すことができます。

\begin{equation} \alpha_x = \frac{\ce{[ML_x]}}{\mathrm{[M_{tot}]}} = \frac{\beta_x\ce{[M][L]}^x}{\mathrm{[M_{tot}]}} = \frac{\beta_x\ce{[L]}^x}{1 + \beta_1\ce{[L]} + \beta_2\ce{[L]^2} + \cdots + \beta_n\ce{[L]^n}} \end{equation}

この関係式を上で紹介した $\ce{[Fe(OH2)6]^{2+}}$ への bpy 置換反応に適用してグラフ化すると以下のようになります。左右は同じデータのプロットですが，右のグラフは縦軸を対数軸で表しています。

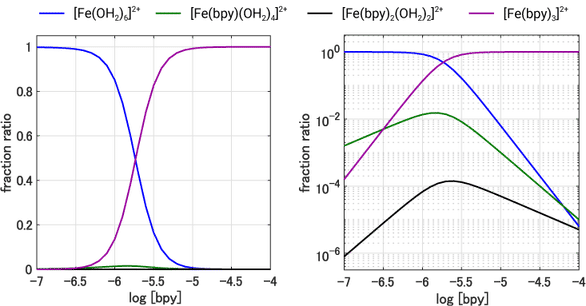
これを見ると bpy 濃度を大きくするにつれて，一段階目の反応生成物である $\ce{[Fe(bpy)(OH2)4]^{2+}}$ の生成（緑線）はわずかに確認できるものの，二段階目の $\ce{[Fe(bpy)2(OH2)2]^{2+}}$（黒線）は対数軸にしないと見えないくらいに微量しか生成せず，最終生成物である $\ce{[Fe(bpy)3]^{2+}}$ の生成が支配的であることがわかります。つまり一つ目が反応したら，一気に三つ目まで反応が進行してしまうことが分かります。そしてグラフから bpy の濃度が $10\unit{\mathrm{\mu mol\,dm^{-3}}}$ 以上であれば溶液中にはほぼ $\ce{[Fe(bpy)3]^{2+}}$ だけが存在しているということを読み取ることができます。右側の対数軸グラフを見ると，bpy 濃度が $10^{-6.5}\molL$ くらいまでの極めて低濃度の領域では一置換体 $\ce{[Fe(bpy)(OH2)4]^{2+}}$ の生成（緑線）がわずかに優勢ですが，それ以上の濃度ではまだ未反応の $\ce{[Fe(OH2)6]^{2+}}$ がたっぷりある状況にもかかわらず，$\ce{[Fe(bpy)(OH2)4]^{2+}}$ や $\ce{[Fe(bpy)2(OH2)2]^{2+}}$ はマイナー成分で，$\ce{[Fe(bpy)3]^{2+}}$ の生成が圧倒的であることが分かります。

上の表で紹介した四つの反応についても，溶液中の配位子 $\ce{L}$ の濃度に対して，その溶液中に含まれる各置換体の存在比がどうなるかをグラフ化してみましょう。生成定数の違いを反映して，四者四様とでも言うべき結果となりました。

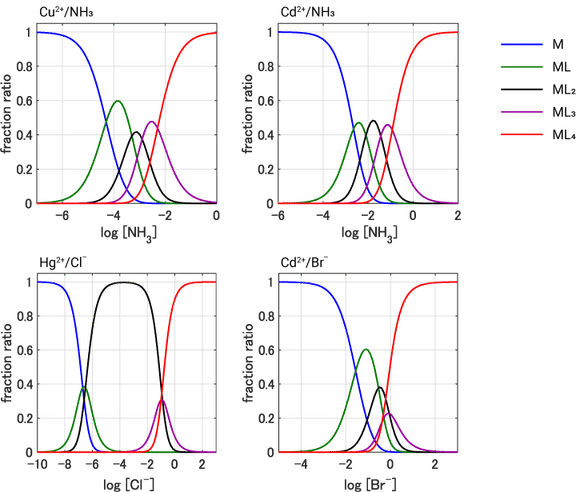
水和金属イオンの多段階置換反応における配位子濃度と生成化学種の関係