配位子場理論3
ここでは錯体が正八面体 $\grp{O}{h}$ 型以外の構造をとるときの配位子場分裂を考えます。理論的な背景を考えるには,群論の知識が必要になりますが,ここでは結果のみを記すことにします。
四配位正四面体型(T-4)
結晶場の説明の際に,四配位正四面体型の結晶場分裂を結果のみ示しました。ここでは配位子場に基づく結論をまとめます。錯体が正四面体の $\grp{T}{d}$ 対称であるとき,$\sigma$ 結合および $\pi$ 結合に関わる配位子のグループ軌道の対称性は,群論を用いた考察により,それぞれ $\irrep{a}{1}+\irrep{t}{2}+{e}{}$ および $\irrep{t}{1}+\irrep{t}{2}$ となります。一方,金属イオンの $\ao{s}$ 軌道は $\irrep{a}{1}$ 対称,$\ao{p}$ および $\ao{d}_{xy}$,$\ao{d}_{yz}$,$\ao{d}_{zx}$ 軌道は $\irrep{t}{2}$ 対称,そして $\ao{d}_{x^2-y^2}$,$\ao{d}_{z^2}$ 軌道は $\irrep{e}{}$ 対称ですので,$\ao{d}_{xy}$,$\ao{d}_{yz}$,$\ao{d}_{zx}$ 軌道は $\ao{p}$ 軌道と同じ対称性を有し,これらは混合して $\sigma$ 結合を形成します。
四配位平面型(SP-4)
四配位錯体には正四面体型の他に,平面四角形型の構造をとるものもあります。この構造は,正八面体型構造の trans 位にある二つの配位子を中心金属から無限遠に遠ざけることで作ることができます。遠ざける二つの配位子が $z$ 軸上にあるとすると,配位子を遠ざけることで $z$ を含む $\ao{d}$ 軌道が安定化し,相対的に $z$ を含まない軌道が不安定化します。その結果,$\ao{d}_{x^2-y^2}$ 軌道と $\ao{d}_{xy}$ 軌道は不安定化し,$\ao{d}_{z^2}$ 軌道と $\ao{d}_{yz}$,$\ao{d}_{zx}$ 軌道は安定化します。安定化や不安定化の程度は配位子がどのくらい遠ざかるかに依存しますので,どこかで $\ao{d}_{z^2}$ 軌道のエネルギーと $\ao{d}_{xy}$ 軌道のエネルギーが逆転します。これをまとめたのが以下の図です。
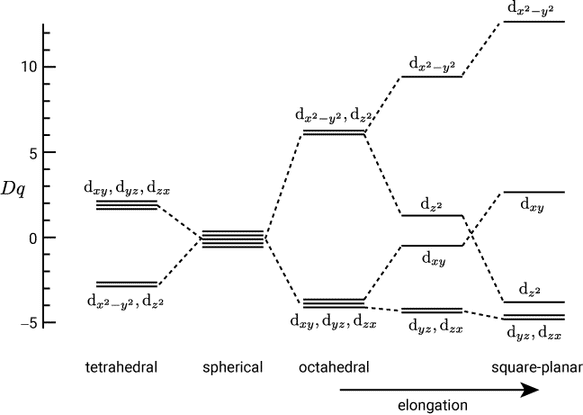
四配位配位子場

